机器学习算法系列（19）XGBoost

XGBoost是GBDT的一种高效的实现，它是由华盛顿大学的陈天奇开发的一个高度可扩展的、端到端的提升系统。近几年XGBoost在各大算法竞赛中取得的成绩一时间可谓风头无两，它取得成功背后在于它在所有场景中的可扩展性，它在处理稀疏数据上的标点也是非常强大的。

1. 回顾提升树（Boosting Tree）

提升树（Boosting Tree）是集成学习的代表之一，在之前的文章中我们就提到过，集成学习的本质：单个单个的基学习器表达能力弱没有关系，只要把它们组合起来了就可以很强大了，可以概括为“三个臭皮匠顶个诸葛亮”。

提升树实际上是K个弱学习器的线性组合而得到的加法模型，所谓提升（Boosting）的本意是在上一个弱学习器的基础上更进一步缩小与目标值的距离，使用公式可以表示为（来自陈天奇的论文）：

简单解释一下，数据集中的每一条数据都会落入弱学习器叶子结点的某一个区域，即对应的预测值，然后最终的预测结果等于所有树的预测值之和。如下图，小男孩（代表数据集中的一条数据）最终的预测结果为tree1和tree2预测值之和：

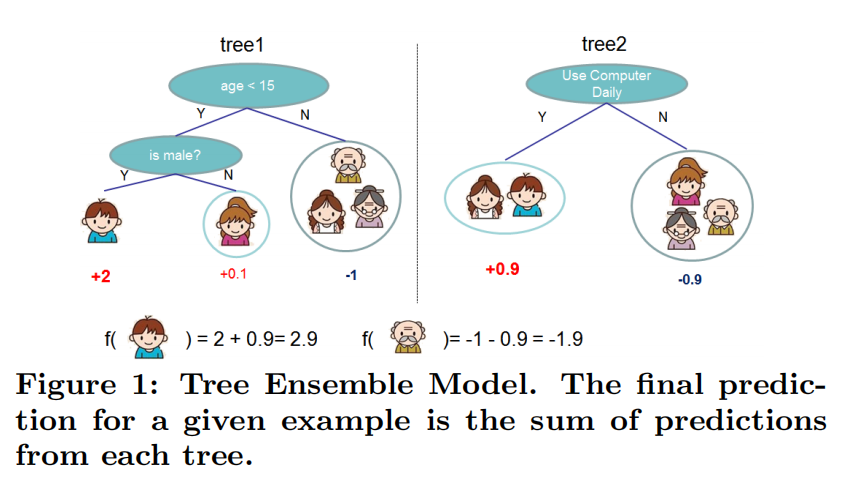
2. XGBoost损失函数的优化求解过程

以上就是对提升树模型的简要回顾，下面正式进入XGBoost的部分，首先看XGBoost的损失函数：

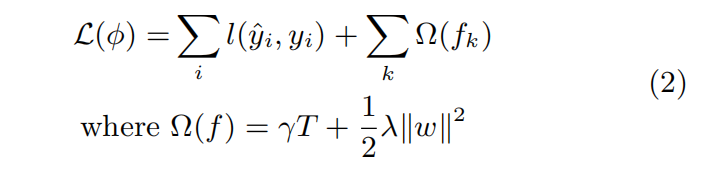
回顾GBDT的损失函数：

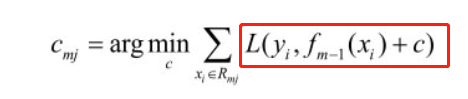
可以看出，相比GBDT，XGBoost在其基础上添加了正则化项$\Omega(ht) = \gamma J + \frac{\lambda}{2}\sum\limits{j=1}^Jw{tj}^2$，正则化项中的$w{tj}$对应第$t$个弱学习器第$j$个叶子节点的最优值，与GBDT损失函数中的$c$是相同的意思（陈天奇的论文中是用$w$表示的，意思一样），$J$指的是叶节点的个数，$\gamma$和$\lambda$都是超参数。在损失函数中添加正则化项的有助于降低模型的复杂性和防止模型出现过拟合的情况。

接下来问题来了，如何最小化XGBoost的损失函数呢？对于公式（2），如果节点的分裂使用的是均方误差那很好优化，而XGBoost损失函数却无法通过一般的凸优化方法来求解，因为它实质上是一个NP hard的问题，因此XGBoost使用的贪心法来获得优化解，每次节点的分裂都期望最小化损失函数的误差，所以XGBoost的损失函数中加入了当前的树$f_t$，损失函数变成：

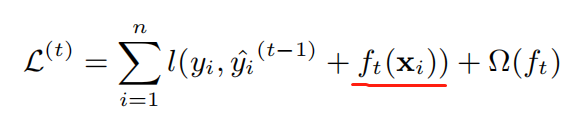
然后对该损失函数做泰勒的二阶展开得：

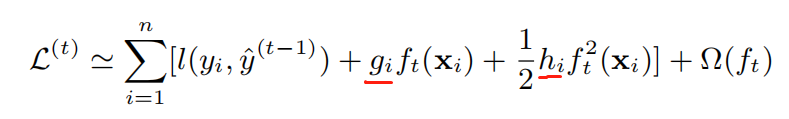
其中$g_i$和$h_i$是第i个样本在第t个弱学习器对$\hat{y}^{(t-1)}$一阶偏导和二阶偏导，由于损失函数中的$l$是常数，在最小化中可以去掉，上面的式子可以进一步写成：

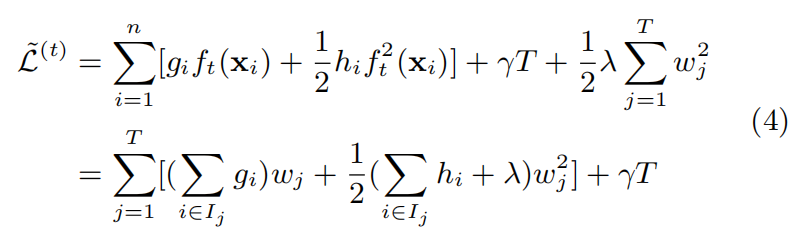
以下是公式（4）的推导改写过程，将n条数据全部代入目标函数后，可以将式子从叶节点的角度改写一下

对于公式（4）的$w_j$的求解比较简单，损失函数对$w_j$求导并令其为0，可得最优解$w_j^{*}$：

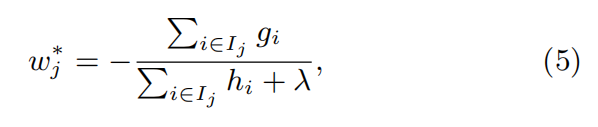
然后将最优解代入公式（4），可得：

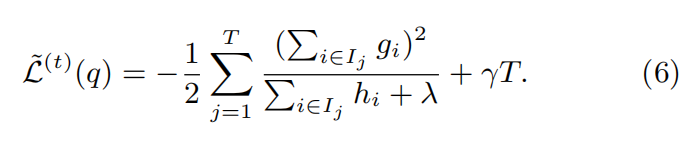
接着，每次在节点做左右子树分裂split的时候，我们要尽量减少损失函数的损失，也就是说，假设当前节点左右子树的一阶、二阶导数和为$G_L,H_L,G_R,H_R$，我们期望最大化下式（为什么是期望最大化下面会解释）：

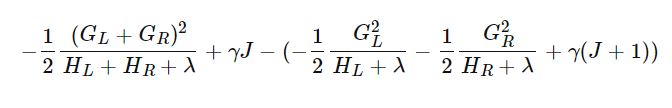
整理，得：

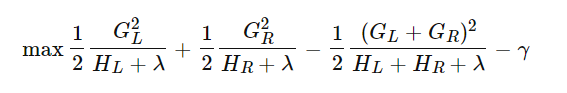
这里有一个疑问，上面的这个式子是怎么从公式（6）计算得来的呢？自己想了很久没有想清楚，在B站上找到了一个up主把节点分裂的过程解释得非常到位！看下图，现在假设我们有从1到8的8个样本点。

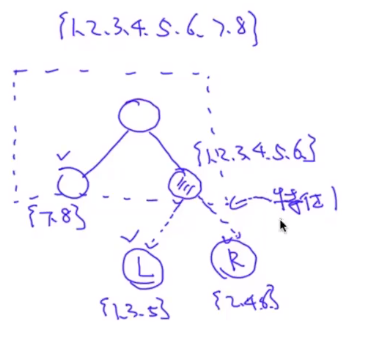
第一次分裂，左子树两个样本点{7,8}，右子树有六个样本点{1,2,3,4,5,6}，此时的目标函数为：

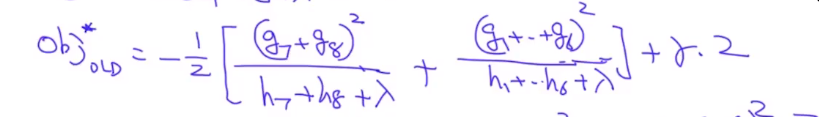
接下来，我们选择某个特征对右子树做节点分裂，假设分裂的结果为左子树为{1,3,5}，右子树为{2,4,6}，此时的目标函数为：

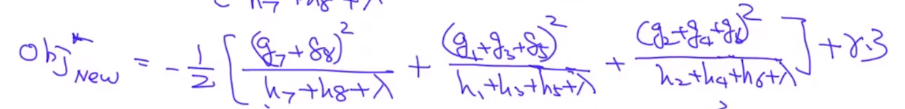
在节点向下分裂的过程中，我们希望第二步目标函数变得越来越小，故实际上我们期望最大化的是第一步的目标函数减去第二步的目标函数：（这里请重点理解！）：

到此，XGBoost损失函数的优化求解就记录得差不多了。

3. XGBoost的训练过程

计算所有m个样本对于当前轮损失函数的一阶导数$G$和二阶导数$H$
基于当前节点分裂决策树，初始化score为0，如果当前有$k$个特征：
1. 样本按照第k个特征排好序，放入左子树，然后计算左右子树一阶和二阶导数和
2. 更新score
基于score最大的特征分裂

4. XGBoost类库的参数

在梯度提升决策树的文章的末尾提到了GBDT在sklearn中可以调节的参数，其实XGBoost和GBDT可调节的参数都差不多。

通用参数：

booster ：弱学习器种类，gbtree或者dart
objective：损失函数，如果是回归问题一般使用reg:squarederror，分类问题使用binary:logistic或者multi:softmax，另外还可以通过设置损失函数决定模型的输出是概率还是原始的预测值
n_estimators：弱学习器的个数，决定了模型的复杂程度，通常和学习率参数一块调参

弱学习器参数：

eta [default=0.3, alias: learning_rate]：学习率，默认等于0.3
gamma [default=0, alias: min_split_loss]：等于目标函数中正则化项的gamma，决策树分裂时最大化下式时必须大于gamma才能继续分裂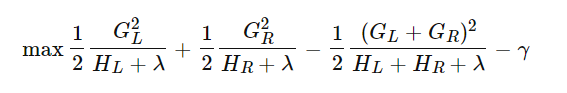
max_depth [default=6]：定义树的最大深度，决定了模型的复杂程度，通常需要通过网格搜索决定最佳的树的深度
min_child_weight [default=1]：决策树中子节点最小的权重阈值，如果子节点的权重阈值小于min_child_weight则不再继续分裂
subsample [default=1]：训练集的采样率，介于0,1之间
sampling_method [default= uniform]：采样方法，有uniform和gradient_based
colsample_bytree, colsample_bylevel, colsample_bynode [default=1]：针对特征采样的手段，层级别、树级别和子节点级别，采样率介于0,1之间
lambda [default=1, alias: reg_lambda]：L2正则化系数，对应$\Omega(ht) = \gamma J + \frac{\lambda}{2}\sum\limits{j=1}^Jw_{tj}^2$里面的$\lambda$
alpha [default=0, alias: reg_alpha]：L1正则化系数，对应$\Omega(ht) = \gamma J + \frac{\lambda}{2}\sum\limits{j=1}^Jw_{tj}^2$里面的$\gamma$
tree_method：默认auto，自动选择最快的方法