从扑克牌的角度理解排序算法（一）

发表于 | 更新于 | 分类于 | 阅读次数：

credit by Josh Appel

快速排序

快速排序用到了“分而治之”的思想，即先解决小问题，然后再将小问题挨个合并，这种思想在归并排序中也有体现。

想象我们手中有一手未排序的扑克牌，如何用快速排序的方法对它排序呢？首先，需要选择一张牌作为基准（pivot），选择的方式有多种，为了方便起见，就拿第一张作为基准牌。基准牌的作用是用来切割扑克牌，我们约定比它小的全部放在它左边（less），比它大的全部放在它右边（more）。经过第一次的切割之后，基准牌的左边都是比它小的，右边都是比它大的，但是左右两边依然是无序的。

然后仍旧递归地对左边和右边重复以上的操作，直到左边和右边的长度都小于等于1，此时排序结束，返回 left + pivot_list + right。

常见的快速排序递归版本，这个版本的快速排序比较容易理解，但是要求分配额外的内存空间：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def quick_sort(list):
    
    less = []
    more = []
    pivot_list = []

    if len(list) <= 1:
        return list

    else:
        pivot = list[0]
        for item in list:
            if item < pivot:
                less.append(item)
            elif item > pivot:
                more.append(item)
            else:
                pivot_list.append(pivot)
        # 对左边和右边分别递归
        less = quick_sort(less)
        more = quick_sort(more)
        return less + pivot_list + more

另外一个版本，这个是不需要额外分配空间的原地排序。原地排序版本的快速排序的关键在于切分（partition）的操作，它在数组中找到一个哨兵值（pivot），使得在数组中哨兵值的左边都小于哨兵值，而数组的右边都大圩哨兵值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# in-place
def partition(array, lo, hi):
    i = lo + 1         # 左指针
    j = hi             # 右指针
    pivot = array[lo]  # 哨兵值
    
    while i <= j:
        while array[i] < pivot and i < j:  # 直到找到一个*大于等于*哨兵值的元素
            i += 1                         # i<j是为了防止当哨兵值是最大值时左指针越界
        while array[j] > pivot:            # 直到找到一个*小于等于*哨兵值的元素
            j -= 1                         # 切分元素不可能会比自己小，右指针不会存在越界情况

        if i < j:                          # 左右指针未相遇，交换位置
            array[i], array[j] = array[j], array[i]
            i += 1
            j -= 1
        else:                              # 左右指针相遇
            i += 1

    array[lo], array[j] = array[j], array[lo]  # 将哨兵值和左子数组最右侧元素array[j]交换，返回j
    return j
    
    
def qsort_inplace(array, lo, hi):
    if hi <= lo:
        return 
    pivot = partition(array, lo, hi)
    qsort_inplace(array, lo, pivot-1)
    qsort_inplace(array, pivot+1, hi)

有人可能会问，这两个版本的快速排序有什么区别吗？第一个版本的看起来更加容易理解啊，但是有一个很大的缺陷，你会发现这种实现的方法额外地分配了空间，it’s not worth the cost。

冒泡排序

想象你手中有一副牌，从最左边第一张牌开始，将第一张牌与第二张牌比较大小，如果第一张牌大，那么交换两者的位置，否则，保持两者不动。然后到第二张牌与第三张牌比较，第三张与第四张比较，以此类推。经过第一轮相邻比较，我们找出了手中最大的一张牌，然后继续对剩下的牌重复上面的步骤。

之所以称之为冒泡排序，经过一轮一轮的比较，越小的数字会逐渐“浮现”到数组的顶端。下面的冒泡排序的实现：

1
2
3
4
5
6
def bubble_sort(array):
    for i in range(len(array)-1, 0, -1):
        for j in range(i):
            if array[j] > array[j+1]:
                array[j], array[j+1] = array[j+1], array[j]
    return array

插入排序

想象自己打扑克牌时理牌的过程，开始手上没有一张牌，摸到一张牌array[0]放在手上（假定是有序的，并且保证手中的牌始终有序的），再摸一张牌，与手上的牌array[0]比较，小的放后面，大的放前面。在打扑克时使用插入排序的人看起来比较小心谨慎还有追求稳定，他们生怕自己手中的扑克牌没有按照顺序排序，使用这种排序算法的老人居多。

插入排序

1
2
3
4
5
6
7
8
9
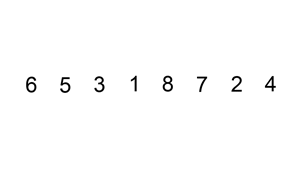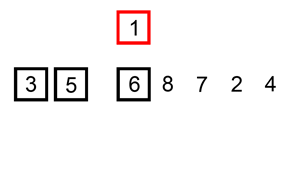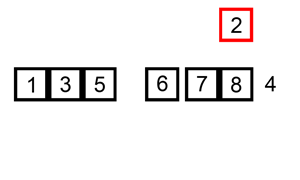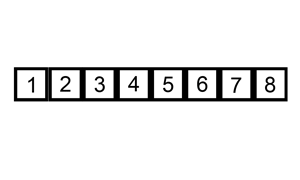
def insert_sort(array):
    for i in range(1, len(array)):
        new_card = array[i]  # 手中的牌
        j = i - 1
        while j >= 0 and new_card < array[j]:  # 新摸到的牌如果大于手中的牌则往后移动
            array[j+1] = array[j]
            j -= 1
        array[j+1] = new_card
    return array

Python-算法]python实现冒泡，插入，选择排序 - CSDN博客

选择排序

我在观察大人打扑克牌的时候发现，我小舅舅在摸牌时并不会像其他人用“插入排序”，他的策略是在所有牌摸完之前不给牌排序。等到所有的牌都到手后，他开始使用“选择排序”。

首先从第一张牌开始，假定第一张牌是最小的，然后将所有的牌与第一张牌比较，找到真正最小的牌并跟第一张牌交换，每次循环找出一个最小值。由此看来，冒泡排序和选择排序差不多，但是两者的复杂度还是有区别的，在最坏的情况，冒泡排序需要 $O(n^{2})$次交换，而插入排序只要最多$O(n)$交换。

下面是选择排序的实现：

1
2
3
4
5
6
7
8
def select_sort(array):
    for i in range(0, len(array)-1):
        min = i
        for j in range(i+1, len(array)):
            if array[j] < array[min]:
                min = j
        array[min], array[i] = array[i], array[min]
    return array

归并排序

同快速排序，归并排序也用到了“分而治之”的思想，归并排序的过程是一分一合，“分”指的是先把子序列变成有序，“治”指的是合并各对有序的子序列，使其变成一个整体，它是将两个排好序的数组合并为一个数组的过程。

归并排序

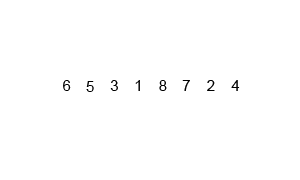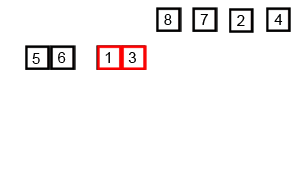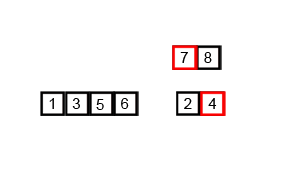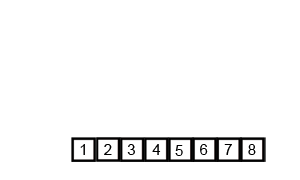
下面是归并排序的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Recursively implementation of Merge Sort
def merge(left, right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    if left:
        result += left
    if right:
        result += right
    return result

def merge_sort(L):
    if len(L) <= 1:
        # When D&C to 1 element, just return it
        return L
    mid = len(L) // 2
    left = L[:mid]
    right = L[mid:]

    left = merge_sort(left)
    right = merge_sort(right)
    # conquer sub-problem recursively
    return merge(left, right)
    # return the answer of sub-problem

if __name__ == "__main__":
    test = [1, 4, 2, 3.6, -1, 0, 25, -34, 8, 9, 1, 0]
    print("original:", test)
    print("Sorted:", merge_sort(test))

图解排序算法(四)之归并排序 - dreamcatcher-cx - 博客园

下面来看另外一个版本的归并排序，不过加入了指针的概念：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def merge(left, right):
    
    result = [None] * (len(left) + len(right))  # 创建临时数组，长度为左右两个数组长度之和
    i, j, k = 0, 0, 0
    
    while i < len(left) and j < len(right):
        if left[i] < right[j]:    # 当左数组元素*小于*右数组元素，则将该元素放入result数组，同时左指针右移
            result[k] = left[i]
            i += 1
        else:                     # 当左数组元素*大于*右数组元素，则将该元素放入result数组，同时右指针右移
            result[k] = right[j]
            j += 1
        k += 1
    
    while i < len(left):          # 左右两个子数组长度不相等，则将剩余的部分全部放入result
        result[k] = left[i]
        i += 1
        k += 1
        
    while j < len(right):
        result[k] = right[j]
        j += 1
        k += 1
    
    return result

def merge_sort(array):
    
    if len(array) <= 1:
        # When D&C to 1 element, just return it
        return array
    
    mid = len(array) // 2
    left = array[:mid]
    right = array[mid:]

    left = merge_sort(left)
    right = merge_sort(right)

    return merge(left, right)
    # return the answer of sub-problem

if __name__ == "__main__":
    test = [1, -1, 3, 2]
    print("original:", test)
    print("Sorted:", merge_sort(test))
------本文结束，欢迎收藏本站、分享、评论或联系作者！------
相关文章
点击查看
赠人玫瑰 手有余香
0%