排序算法（二）：堆排序

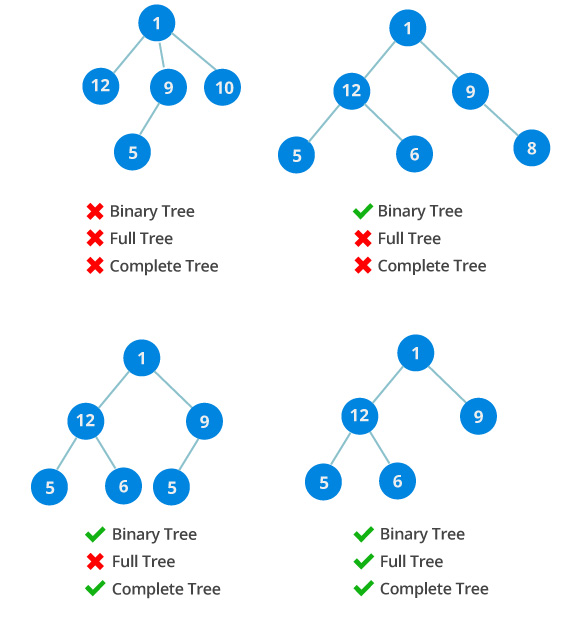
完全二叉树的特点（百度百科）：

一棵二叉树至多只有最下面的两层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，则此二叉树成为完全二叉树，并且最下层上的结点都集中在该层最左边的若干位置上，而在最后一层上，右边的若干结点缺失的二叉树，则此二叉树成为完全二叉树。

完全二叉树具备以下特点：

叶子节点只能出现在最下两层
最下一层的的节点可能没有右子节点，如果只有一个节点，那么它必须是左子节点
除了最下面两层，每个节点必须有且仅有两个子节点

从完全二叉树回到堆排序，堆排序分为三个步骤：

首先，我们需要从已有的数组构建最大堆，然后，已有数据的最大值会位于堆的最顶端（root node）
最大堆一旦建立，将最大值（root node）与数组最后一个元素交换，并从堆中删除最后一个node
只要堆的大小大于1，重复1-2步骤

堆排序的时间复杂度：

堆排序是一种原地排序（inplace）算法，不需要分配额外的内存空间，它的运行时间主要消耗在了构建堆和重建堆时的反复筛选上了，它对原始数据的排序状态并不敏感，总体来说，无论是最好、最坏还是平均，堆排序的时间复杂度都为$O(nlogn)$。

下面是堆排序的Python实现：

# Python program for implementation of heap Sort 
  
# To heapify subtree rooted at index i. 
# n is size of heap 
# heapify()函数的作用是对索引i下的子树构建最大堆
def heapify(arr, n, i):  # n是堆的大小，先假设i是根节点
    largest = i          # Initialize largest as root 
    l = 2 * i + 1        # left = 2*i + 1 
    r = 2 * i + 2        # right = 2*i + 2 
    
    # See if left child of root exists and is 
    # greater than root 
    if l < n and arr[i] < arr[l]: 
        largest = l 
  
    # See if right child of root exists and is 
    # greater than root 
    if r < n and arr[largest] < arr[r]: 
        largest = r 
  
    # Change root, if needed
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # 如果发现左右子节点中有大于根节点的，则互换其位置
  
        # Heapify the root. 
        heapify(arr, n, largest)                     # 继续对子树构建最大堆
  
# The main function to sort an array of given size 
def heapSort(arr): 
    n = len(arr)
  
    # Build a maxheap. 
    for i in range(n, -1, -1):  # 从完全二叉树最低端的叶子节点往根节点遍历，构建最大堆，时间复杂度为O(n)
        heapify(arr, n, i)      
  
    # One by one extract elements 
    for i in range(n-1, 0, -1):          # 数组中最大的元素永远在堆的最顶端，下标为0
        arr[i], arr[0] = arr[0], arr[i]  # 找出树中的最大元素，与最后一个node交换
        heapify(arr, i, 0)               # 重新构建最大堆，此时i是数组的长度，已经不包含最后一个最大的元素了
  
# Driver code to test above 
arr = [ 12, 11, 13, 5, 6, 7] 
heapSort(arr) 
print ("Sorted array is", arr) 
# This code is contributed by Mohit Kumra