通常,我们为了追求模型在训练集上的表现,在模型中加入了过多的参数,它通过“死记硬背”式的方式学到了很多东西。但是,往往数据中也是存在噪声的,模型把这些噪声也学到了,导致当它去预测新数据的时候预测能力不佳。
The general principle is we want both a simple and predictive model. The tradeoff between the two is also referred as bias-variance tradeoff in machine learning.
通常我们需要一个简单并且预测能力强的模型,这两者之间的权衡通常就是指机器学习中偏差方差的权衡。
如何达到这个目的?正则化!
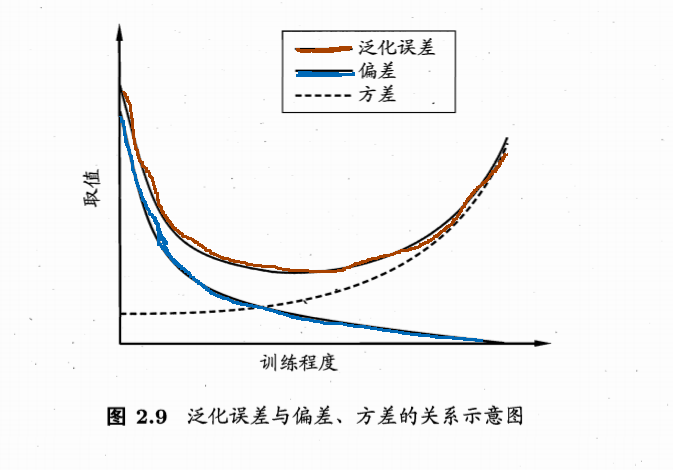
关于偏差和方差,更多:如何解释方差与偏差的区别?
了解正则化之前,有必要弄明白范数,不太严谨地解释:
- 0 范数,向量中非零元素的个数。
- 1 范数,为绝对值之和。$||\beta||$
- 2 范数,就是通常意义上的模。${||\beta||}^2$

正则化的目的是为了控制模型的复杂度,即通常所说的过拟合,实际上是 bias 和 variance 之间的一个 tradeoff,往往模型的 bias 很低,但是一接触到新的数据就表现不太好(泛化能力不佳)。既然,我们需要一个简单并且预测能力强的模型,正则化如何达到这个目的呢?L1 正则化是可以减少特征的数量,L2 正则化则是可以降低特征的权重。
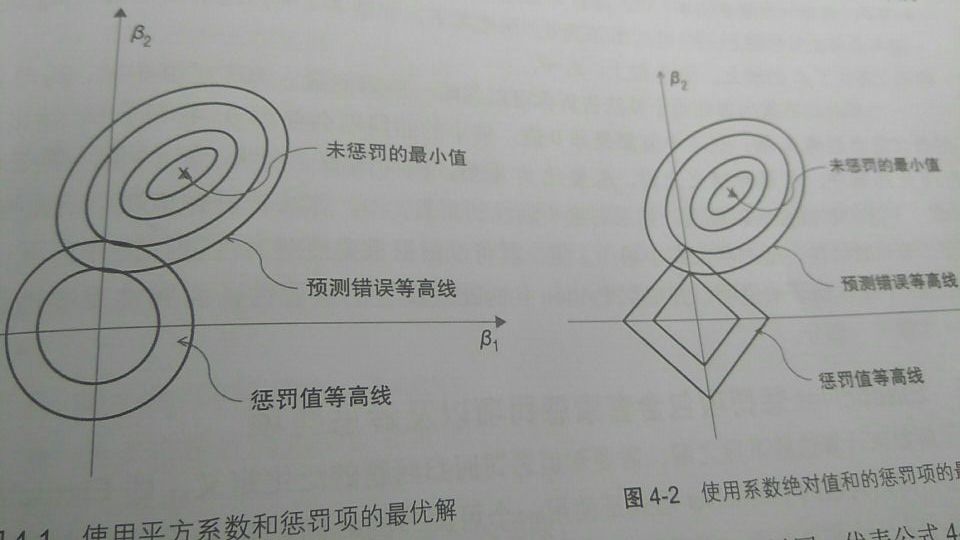
这两者有什么不同呢?两者优化得到的解有差别,从图中来看,L2 正则化的最优解,即预测错误(损失函数)等高线与惩罚值等高线(正则化项)的相交点,最优解的点比较随机,此时 $\beta_1$ 和 $\beta_1$ 的值不一定为零。 观察 L1 正则化,两条等高线的相交点出现在坐标轴处,这就意味着特征必有一个为零(该例中 $\beta_1$ 等于零)最优解出现的地方往往出现在某个轴。
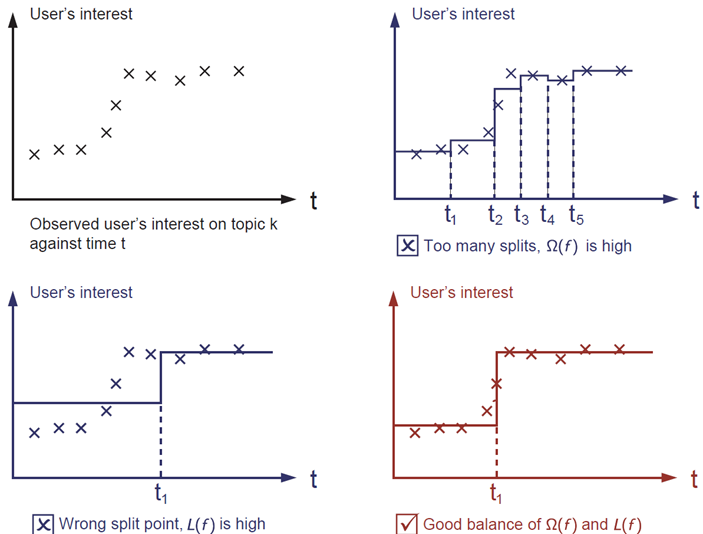
特征多了不好,模型的泛化能力不强。特征少了也不行,模型的预测能力太弱。

