【译】数据科学家降维技术测试 40 题

原文链接：https://www.analyticsvidhya.com/blog/2017/03/questions-dimensionality-reduction-data-scientist/

前言

你有没有遇到过拥有几百列的数据集而对其建立预测模型不知所措？或者数据集的变量大量相关？在现实的工程问题中这些问题是很难避免的。

幸亏，降维技术帮了我们大忙，在数据科学中，降维是一门很重要的技术。对于任何数据科学家来说，降维技术是必备的。为了检测我们在降维技术中的知识，我们组织了这次技能测试。这些问题包括主成分分析、t-SNE 和 LDA。

Q & A

1. 假如你在机器学习问题中有 1000 个输入特征和一个目标特征，基于输入特征和目标特征之间的关系，要求你选出100个最重要的输出特征，请问这是一个降维的例子吗？

   • 是
   • 否

2. 【判断题】在应用降维算法时没有必要设置目标变量【对】

   • 解析：LDA 是有监督降维算法

3. 数据集中有 4 个变量 A、B、C、D，执行下列步骤

   • step1：使用以上变量创建两个新的变量，$E=A+3B$ 和 $F = B + 5*C + D$

   • step2：只用 E 和 F 两个变量建立随机森林模型

     问：以上步骤是否属于降维手段的一种

   • 对
   • 错
   • 解析：因为在第一个步骤中使得数据降低到只有两个维度
4. 下列哪种方法降维的效果更好？
   • A. 去除缺失值多的列（如果数据集中某一列缺失值太多，可以肯定的是一定要去掉）
   • B. 去除高方差的列
   • C. 去除数据趋势不同的列
   • D. 以上都不是
5. 【判断题】降维算法是建立模型时减少运算时间的一种可行方法。【对】
6. 下列哪种算法不能用于数据的降维？
   • A. t-SNE
   • B. PCA
   • C. LDA False
   • D. 以上都不是
7. 【判断题】PCA 可用于将数据映射和可视化到低维空间。【对】
   • 有的时候有必要将数据集在低维空间中可视化出来，我们可以用前两个主成分并画出它们的散点图
8. PCA 是非常受欢迎的降维算法，下列对于PCA的说法正确的是？【全部都是】
   1. PCA 是无监督方法
   2. 寻找原始数据中方差最大的方向（原理解释参考：机器学习算法系列（10）主成分分析（PCA））
   3. 主成分最大个数小于等于特征个数
   4. 所有的主成分相互正交（协方差矩阵是对称的）

9. 假设用降维算法给数据预处理，将数据降到只有 k 个维度之后，然后用这些 PCA 映射作为特征，下列陈述正确的是？

   • A. k 越大则正则化效果越强
   • B. k 越大则正则化效果越弱（k 越大意味着要保留数据中的更多特征，所以正则化效果越弱）

10. 考虑一台计算能力不强的计算机，下列哪种降维场景中，t-SNE 比 PCA 表现得要好？

    • A. 数据集有 100 万 entries，300 个特征
    • B. 数据集有 10 万 entries，310 个特征
    • C. 数据集有 1 万 entries，8 个特征
    • D. 数据集有 1 万 entries，200 个特征

    t-SNE 有着$O(n^2)$的时间和空间复杂度，考虑计算能力有限的系统资源，则必须选择 c，因为它只有 8 个特征，并且在这样一个小特征的数据集降维重要信息的丢失是很少的

11. 对于 t-SNE 的损失函数，下列陈述正确的是？

    • A. 不对称
    • B. 对称
    • C. 与SNE的损失函数一样

    SNE的损失函数本质上是不对称的，故使用梯度下降算法很难收敛。损失函数是不是对称是 SNE 与 t-SNE 最大的区别

12. 假设在处理文本数据中使用词嵌入（Word2vec），得到一个 1000 个维度的词向量。现在，你想要降低它的维度，这样最近邻空间的单词具有同样的含义。在这种情况下，你会选择哪个算法？

    • t-SNE
    • PCA
    • LDA

13. 【判断题】t-SNE 学习的是非参映射【对】

14. 对 PCA 和 t-SNE 说法正确的是
    • t-SNE 是线性的，PCA 是非线性的
    • t-SNE 和 PCA 都是线性的
    • t-SNE 和 PCA 都是非线性的
    • t-SNE 是非线性的，PCA 是线性的
15. 在 t-SNE 算法中，哪个高维参数可以调参？
    • 维度的个数
    • Smooth measure of effective number of neighbours
    • 最大迭代次数
    • 以上所有
16. t-SNE 与 PCA 相比，下列说法正确的是？
    • 数据集很大的时候，t-SNE 可能产生不了较好的结果
    • 不管数据集大或者小，t-SNE 总能产生更好的结果
    • 针对小规模数据，PCA 总是比 t-SNE 表现得更好
    • 以上都不是

17. $x_i$和$x_j$是高维数据中的两个不同的点，$y_i$和$y_j$是$x_i$和$x_j$在低维空间的映射

    1. $x_i$和$x_j$的相似度等于条件概率$p(j|i)$
    2. $y_i$和$y_j$的相似度等于条件概率$q(j|i)$
    • $p(j|i)=0$，$q(j|i)=0$
    • $p(j|i) \lt q(j|i)$
    • $p(j|i) = q(j|i)$
    • $p(j|i) \gt q(j|i)$

18. 关于 LDA 正确的是？
    

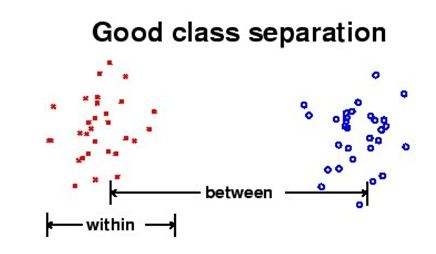
    • LDA 的目标在于最大化不同类之间的距离且最小化相同类之间的距离
    • LDA 的目标在于同时最小化相同和不相同类之间的距离
    • LDA 的目标在于最小化不同类之间的距离且最大化相同类之间的距离
    • LDA 的目标在于同时最小化相同和不相同类之间的距离

19. 哪种情形下，LDA 会失败？

    • 如果 discriminatory information 不在数据的方差中而在均值中
    • 如果 discriminatory information 不在数据的均值中而在方差中
    • 如果 discriminatory information 都在数据的方差和均值中
    • 都不是
20. 下列关于 PCA 和 LDA 的比较,正确的是？
    • LDA 和 PCA 都是线性转换的手段
    • LDA 是监督学习而 PCA 是无监督
    • PCA 最大化数据的方差，而 LDA 最大化不同类别之间的间隔
21. 当特征值都大致相等时？
    • PCA 表现很好
    • PCA 表现不好
    • 不确定

      当特征向量都相同时，在这种情况下你不可能选择主成分因为主成分都是相等的

22. 满足下列哪种条件，PCA 会表现得更好？
    • 数据集有线性结构
    • 如果数据集在弧面而不是平面
    • 变量都在同一个单位空间
23. 低维空间中使用 PCA 得到的特征？
    • 特征仍有解释性
    • 特征将失去解释性
    • 特征一定携带目前数据的所有信息
    • 特征可能没有携带目前数据的所有信息
24. 给定以下高度和重量的散点图，
    
    • 0
    • 45
    • 60
    • 90
25. 下列哪个选项是正确的？
    • PCA 需要初始化参数
    • PCA 不需要初始化参数
    • PCA可能会陷入局部最小化问题
    • PCA 不会陷入局部最小化问题
26. 下图是两个特征的散点图，PCA 和 LDA 的方向，哪种方法能够得到比较好的分类结果？
    
    • 用 PCA 建立分类算法
    • 用 LDA 建立分类算法
    • 不确定

      如果任务的目标是划分点集，PCA 映射会得不偿失

27. 针对图像数据运用 PCA 时，下列哪个选项是正确的？
    • 检测变形的物体会很有效率
    • It is invariant to affine transforms
    • 可以用于lossy图像压缩
    • not invariant to shadows
28. 在何种情形下，SVD 和 PCA 产生一样的结果
    • 数据中位数为 0
    • 数据均值为 0
    • 都是一样的

      如果数据拥有零均值，在使用SVD的时候首先你得center the data

29. 考虑二维空间下的三个数据点，数据的第一个主成分是？
    
    • [$\sqrt2/2, \sqrt2/2$]√
    • [$1/\sqrt3, 1/\sqrt3$]
    • [$-\sqrt2/2, \sqrt2/2$]√
    • [$-1/\sqrt3, -1/\sqrt3$]
30. 如果用主成分把原始数据投影到一维子空间，它的坐标是多少？
    • $(-\sqrt2,0,\sqrt2)$√
    • $(\sqrt2,0,\sqrt2)$
    • $(\sqrt2,0,-\sqrt2)$
    • $(-\sqrt2,0,-\sqrt2)$
31. 根据29-31对于你从$(-\sqrt2,0,\sqrt2)$得到的数据，如果你要将它们呈现在二维空间中，损失会是多大？
    • 0%
    • 10%
    • 30%
    • 40%
32. 在 LDA 中，最理想的是找到划分两个类别的线。在给定图像中哪个映射是最好的？
    
    • LD1
    • LD2
33. PCA 是一门很好的降维技术，因为它易于理解并且被广泛应用。观察f(M)是如何随着M的移动而变化的，见下图。问，上面两幅图中 PCA 的表现更佳？
    
    • 左图
    • 右图

34. 下列哪个选项是正确的？

    • LDA 尝试找出数据类之间的不同，PCA 则不是
    • LDA 和 PCA 两者都尝试找出数据类的不同

35. 应用 PCA 之后，下列选项哪个是前两个主成分？

    • (0.5,0.5,0.5,0.5),(0.71,0.71,0,0)
    • (0.5,0.5,0.5,0.5),(0,0,-0.71,-0.71)
    • (0.5,0.5,0.5,0.5),(0.5,0.5,-0.5,-0.5)
    • (0.5,0.5,0.5,0.5),(-0.5,-0.5,0.5,0.5)

36. 下列哪个选项给出了 LR 和 LDA 之间的差别？

    1. 如果类别都被很好地切割了，LR 的参数估计可能会不太稳定
    2. 如果样本集数据太小并且每个类别数据特征都服从正态分布。在这种情况下，LDA 比 LR 要更稳定

37. 下列两种补偿需要考虑 PCA？
    

    • 垂直补偿（vertical offset）
    • 垂直面补偿（perpendicular offset）

38. 如果你在处理10类别分类问题，LDA 最多可以生成多少个discriminate向量？

    • 20
    • 9
    • 21
    • 10

39. 根据下图，使用 PCA 和最近邻方法构造预测是否为“Hoover”的分类器，需要哪些数据预处理？
    

    1. 将图片中的塔放置在图片中央
    2. 将所有图片处理至相同尺寸

40. 下图中最优主成分数目为多少？
    

    • 7
    • 30（方差最大主成分数目最少）
    • 40