严格地说来,本文涉及的主题并非属于机器学习算法,只是机器学习中的一种降维方法,笔者为了方便,仍旧将其归于机器学习算法系列。在解释奇异值分解的时候,笔者回避了难以理解的矩阵空间变换,而是从数学的角度用简单明了的公式说明。
一、前言
在之前一篇文章中有提到过一种降维方法:机器学习算法系列(10)主成分分析(PCA),在这篇文章中我会介绍另外一种在机器学习中非常著名的降维技术:奇异值分解(Singular Value Decomposition,以下简称 SVD)是机器学习中提取信息或者也叫降维的一种方法,SVD 广泛应用于数据压缩和图像去噪。
其实,奇异值分解等价于主成分分析,核心都是求解$A A^{T}$的特征值以及对应的单位特征向量。
举一个简单易懂的例子:比如,每当学习一门新的学科,想象学科中的各种概念和知识构成了一个巨大的矩阵中的每个元素。为了理解它,你阅读了大量的文献,记了许多笔记,反反复复地理解,然后你明白了哪些部分是无关紧要的,哪些是必考的核心概念,一番去粗取精之后,原本厚厚的教材便可以浓缩为几页笔记。简单地来说,SVD 本质上就是这么一个过程,它能够帮助我们去除矩阵中的冗余信息,只保留最能够代表原矩阵的部分。
那么问题来了,如何进行奇异值分解呢?在这之前,听过一次培训班的笔者在庸师的讲解下,被各种 null space 、Strang’s Diagram 留下了“阴影”,以为 SVD 乃一大难度极高的“绝学”,以至于后来一直没敢去碰。
其实,

最近重拾 SVD ,查找了许多资料,其中来自火光摇曳翻译的一篇文章:奇异值分解(We Recommend a Singular Value Decomposition)在中文世界中广为流传,这篇译文加上原文:We Recommend a Singular Value Decomposition前前后后看了不下30遍,然而笨拙如我,除了记住了“22矩阵奇异值分解的几何实质是:对于任意22矩阵,总能找到某个正交网格到另一个正交网格的转换与矩阵变换相对应”这句话,依旧还是没能弄明白 SVD 到底要干啥。罢了,只能老老实实回去啃论文,Dan Kalman, A Singularly Valuable Decomposition: The SVD of a Matrix, The College Mathematics Journal 27 (1996), 2-23. 这篇论文的第2页和第3页,反复读几遍你会对 SVD 与 EVD 两者有更深的理解。然后,直到遇见统计之都的这篇文章:奇异值分解和图像压缩,看到了公式$\eqref{svd}$才豁然开朗,仿佛一语惊醒梦中人!什么鬼旋转、伸缩、再旋转,这才是 SVD 的精髓啊!!!

二、奇异值分解:从特征值分解的角度
回顾线性代数,我们知道,给定实对称矩阵$A_{n*n}$,对它进行特征分解(eigenvalue decomposition,以下简称 EVD)十分简单,只需要求解$ AV=\lambda V $即可,$V$是它的特征向量,$\lambda$是特征值。忘记这部分的读者可以翻翻之前的教材或者看看麻省理工公开课:线性代数,里边有一节专门讲奇异值分解,时隔多年,老爷子去年貌似又更新了
在理解 SVD 前,我们必须抛弃以往在大学学习线性代数时留下的只对或只能方阵做特征分解的思想
考虑任意的$m*n$矩阵$A$,则存在对角矩阵$\Sigma$,正交矩阵$U$和$V$(也叫左右奇异矩阵),有
\begin{equation}\begin{split}
A=U \Sigma V^{T}
\label{1}
\end{split}\end{equation}
奇异值分解的目的就是为了找到符合条件的$\Sigma$,$U$和$V$,使得上式$\eqref{1}$成立。但是,现实中的矩阵大多不是对称矩阵,无法直接求解,所以,奇异值和奇异矩阵的求解需要转换一下思维。
不妨令$A^{T} A =(V\Sigma U^{T}) U \Sigma V^{T}$,由于$U$是正交矩阵,故$U^{T}U$为单位矩阵。所以,有
这样一来,非对称阵的境地就得到了化解,奇异值分解巧妙地转化为特征值分解了。对任意矩阵$A$的 SVD, 右奇异向量是$A^{T} A$的特征向量,左奇异向量是$A A^{T}$的特征向量,奇异值为$\Sigma ^T\Sigma$上对角线非零元素的平方根。

正如上图下划线部分内容,如果$A$本身就是对称矩阵,对$A$的 SVD,它的左右奇异向量等价于$A$的特征向量,它的奇异值等价于$A$的特征值。所以,对任意的$A$,实对称矩阵$A^T A$的 SVD 和 EVD 殊途同归。
讲了这么多,SVD 的求解应该解释得差不多了,不过读者可能还是不明白 SVD 到底是干啥的,你不是说 SVD 可以压缩数据吗?那你是怎么压缩的呢?下面就来从数学的角度来讲讲数据压缩的原理
$A$的左右奇异向量如果用列向量的形式表示
$\Sigma$的对角元素为$\sigma_i$,那么$A$可以分解为一系列的线性组合
\begin{equation}\begin{split}
A = \sigma_1u_1v_1^{T} + \sigma_2u_2v_2^{T}+···+\sigma_nu_nv_n^{T} \
\label{svd}
\end{split}\end{equation}
又因为每项$\sigma_iu_iv_i^{T}$都表示一个$m*n$的矩阵$A_i$。这样一来,我们便可以认为矩阵$A$是$n$个这样矩阵的和。特征值$\sigma_i$越大表示$A_i$对矩阵的贡献越大,所以控制等式右边多项式的个数便可以达到压缩数据的目的!
三、用 Python 实现 SVD
在 Python 下通过 numpy 下的np.linalg.svd()函数可轻松实现 SVD
1 | %matplotlib inline |

1 | # 奇异值分解得左右奇异矩阵和奇异值矩阵 |
下面是图片从压缩到逐步接近原图的过程,可以看出,当只取公式$\eqref{svd}$的前2项时,从图像中几乎不能分辨出 gakki 酱,只能看到一个隐隐约约的轮廓。当奇异值得数目增加到 10 个,似乎能够猜到这是谁了,只是图片仍旧十分模糊。随着奇异值数目的增加,图片越来越清晰。

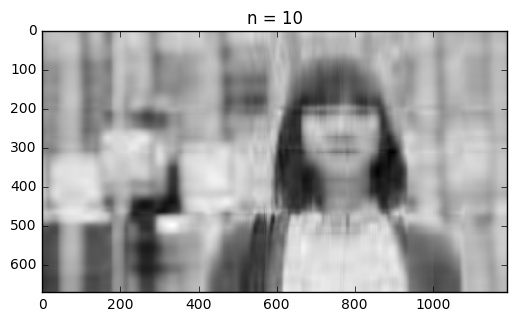

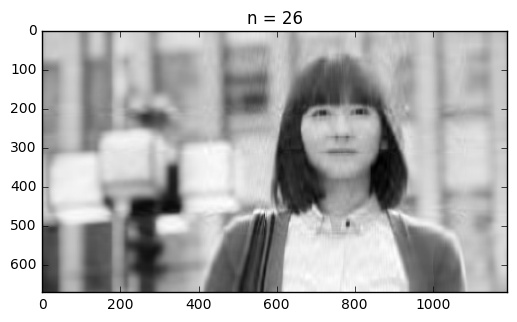

当取了前 51 个奇异值的时候,压缩后的图像与原图基本上看不出什么差别了,这也侧面说明了在 SVD 中,奇异值的分布是很不均衡,绝大多数奇异值集中在一极。以 gakki 的图片为例,总共有 670 个奇异值,奇异值的大小下降特别快,最大的奇异值和第二大的奇异值就相差了一个数量级。

如果您有什么问题或建议,欢迎留言!要是能够帮助分享一下那就再好不过啦!


