主成分分析（Principal Components Analysis，PCA）是一种无监督降维技术，它广泛应用于电视信号传输、图像压缩等领域。当面临的数据维数很高的时候，我们很难发现隐藏在数据中的模式和有用的信息，并且给建模带来不便，PCA 是一种常见的解决这类问题的手段。PCA 的目的在于寻找一个能够对所有样本进行恰当表达的超平面，这个超平面具有两个性质：最近重构性（样本点到这个超平面的距离都足够近）和最大可分性（样本点在这个超平面上的投影能够尽可能分开）。

以上说的可能有点抽象，举个例子，比如晚上你在路灯下行走，当你走到路灯的正底下或者仅仅偏离正底下一点点，光凭一丁点阴影是没有办法判断你的性别的。当你继续往前走，灯光把影子越拉越长，阴影中包含的信息逐渐多了起来，比如胖瘦、头发、衣着等等，此时判断性别就相对简单多了。我举这个例子的用意在于，如果找到一个好的投射坐标系（这是关键！），就能用最小的成本保留原始数据最多的信息。

1. 主成分分析原理

在 PCA 中，数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。

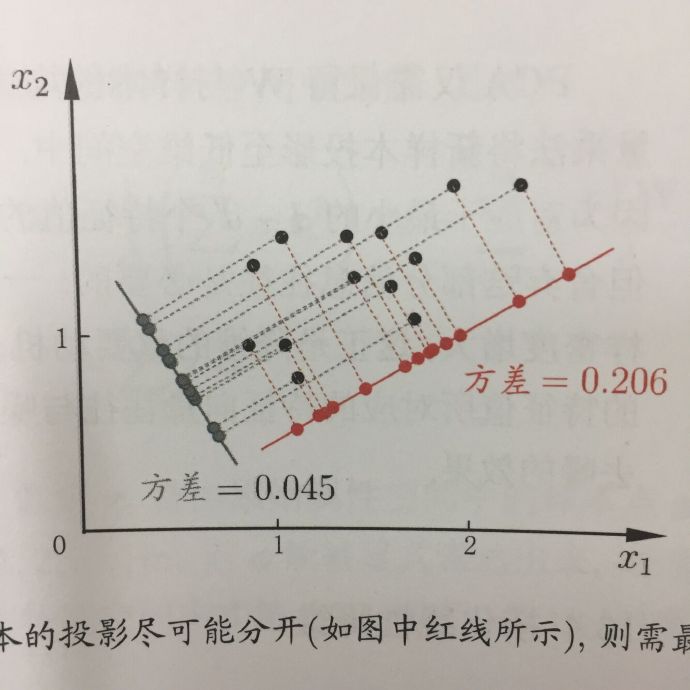
为什么要找原始数据中方差最大的方向？在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如下图，数据投射到红色向量（方差为 0.206）上显然能够更好地将数据隔开，并且能够保留原数据集的最大信息。

图片来源：《机器学习》周志华

PCA的优化目标是什么？假设对数据已经进行了去均值处理$\sum{x_i}=0$，且新坐标系为$W$，并且将维度降低，得到低维坐标中的投影$W^Tx$。因为我们需要尽可能地将样本点分开，所以需要寻找方差最大的方向$W$，由此 PCA 的优化目标

\begin{equation}
max\quad tr(W^TXX^TW) \
s.t.\quad W^TW=I
\end{equation}

然后对上式采用拉格朗日乘子法，

$XX^TW=\lambda W$

是不是很熟悉？这不就是对协方差矩阵$XX^T$求特征值和特征向量嘛！$W$可能包含多个向量，主成分的个数对应着取$W$中多少个特征向量，需要留下多少的信息取决于自身的决定。

2. 预备数学知识

在接触到 PCA 之前，大学学过的线性代数和概率统计的知识有点忘了，在学习的时候顺带把相关的知识复习一下。

2.1 协方差

协方差在概率统计中用于衡量两个变量之间的总体误差，方差是协方差的一种特殊情况。

$cov(X,Y)=\frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{n-1}$ $var(X)=\frac{\sum_{i=1}^{n}(X_i-\bar{X})(X_i-\bar{X})}{n-1}$

如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。

如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

如果两个变量相互独立，那么它们之间的协方差就是零。

上面讨论的情形均是针对两个变量，如果有多个变量的存在呢？比如有$x,y,z$三个变量，那么便需要计算三对协方差，为了方便，我们将协方差放进一个矩阵，称为协方差矩阵（covariance matrix）。

2.2 特征值和特征向量

关于特征值和特征向量的基础知识可参照线性代数第五版（高等教育出版社）“方阵的特征值和特征向量”p117。

3. PCA 基本步骤

了解了一些基本的数学知识之后，便可以开始着手PCA的工作了

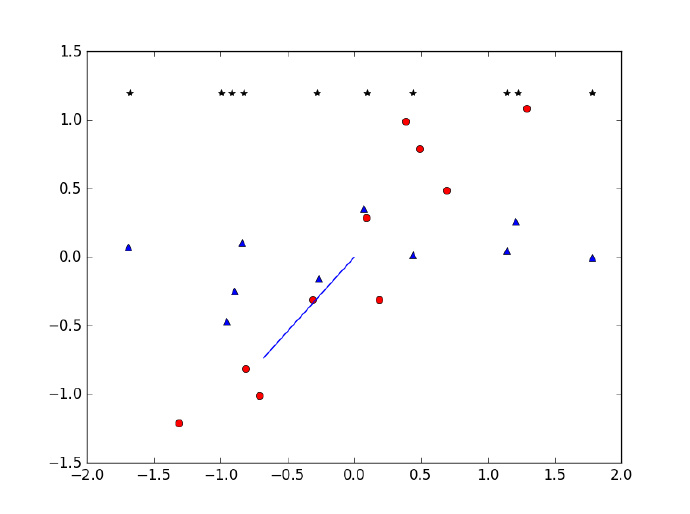
假设我们需要对如下数据做降维处理，需求是将其从2维降到1维，该如何处理呢？

$\begin{array}{c|lcr} Data & \text{} & \text{} \\ \hline x& 2.5&0.5&2.2&1.9&3.1&2.3&2&1&1.5&1.1 \\ y&2.4&0.7&2.9&2.2&3.0&2.7&1.6&1.1&1.6&0.9& \\ \end{array}$

PCA 主要有以下几个步骤：

1.去除平均值，做中心化处理

$\begin{array}{c|lcr} Data\ Adjust & \text{} & \text{} \\ \hline x& .695&-1.31&.39&.09&1.29&.49&.19&-.81&-.31&-.71 \\ y&.49&-1.21&.99&.29&1.09&.79&-.31&-.81&-.31&-1.01 \\ \end{array}$

2.计算协方差矩阵

3.计算协方差矩阵的特征值（eigenvalue）和特征向量（eigenvector）

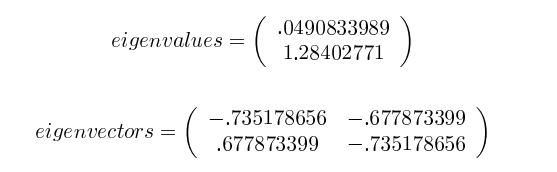
4.将特征值从大到小排列，选择前k个特征值和其相对应的特征向量，并组成新的特征向量矩阵。在本例中只有两个特征值，所以k=1，选择1.28402771和相应的特征向量（Feature vector）$(-0.677873399,-0.735178656)^T$

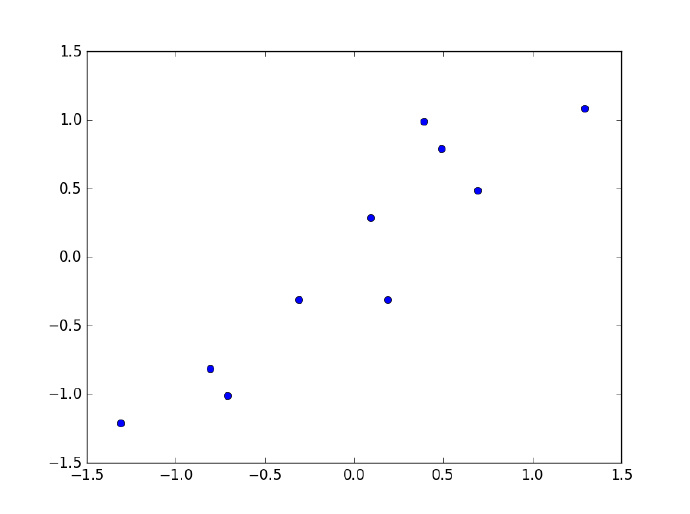
5.将数据集映射到新空间，生成新的数据集。调整后的数据集是 10×2 的矩阵，与特征向量（n×k）相乘之后，原始数据集由 n=2 维变成 k=1 维

$New\ data=Data\ Adjust*Feature\ vector$

降维后的数据集

降维给数据带来了两个影响：

由于维度的降低，较小特征值对应的原始数据的部分信息被舍弃了，数据的采样密度增大，所以对数据降维的目的达到
当数据受到噪声影响时，最小特征值对应的特征向量往往与噪声有关，将它们舍弃能在一定程度上起到降噪的效果

4. 基于 Python 实现 PCA

将上面的例子用 Python 来实现一遍

import numpy as np
import matplotlib.pyplot as plt

# 导入数据，转换为矩阵
x=np.array([2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1])
y=np.array([2.4,0.7,2.9,2.2,3,2.7,1.6,1.1,1.6,0.9])
# 去除平均值
remove_mean_x = x - np.mean(x)
remove_mean_y = y - np.mean(y)
data=np.matrix([[remove_mean_x[i], remove_mean_y[i]] for i in range(len(remove_mean_x))])
plt.plot(remove_mean_x, remove_mean_y, 'o')
plt.show()

去除平均值后的数据

# 计算协方差矩阵
cov = np.cov(remove_mean_x, remove_mean_y)
# 计算特征值和特征向量
eig_value, eig_vector = np.linalg.eig(cov)

计算得到的协方差和特征向量矩阵，协方差矩阵是对称阵，故得到的特征向量之间是相互正交的。

# 协方差矩阵
[[ 0.61655556  0.61544444]
 [ 0.61544444  0.71655556]]
# 特征值
[ 0.0490834   1.28402771]
# 特征向量
[[-0.73517866 -0.6778734 ]
 [ 0.6778734  -0.73517866]]

# 选择特征向量
eig_pairs = [(np.abs(eig_value[i]), eig_vector[:,i]) for i in range(len(eig_value))]
eig_pairs.sort(reverse=True)
feature=eig_pairs[0][1]
# 将数据映射到新空间，得到降维后的数据
rot_data = (np.dot(eig_vector, np.transpose(data))).T
new_data = (np.dot(feature, np.transpose(data))).T

# 降维后的数据
[[-0.82797019]
 [ 1.77758033]
 [-0.99219749]
 [-0.27421042]
 [-1.67580142]
 [-0.9129491 ]
 [ 0.09910944]
 [ 1.14457216]
 [ 0.43804614]
 [ 1.22382056]]

蓝色线条为选择的特征向量，红点为移除平均值之后的数据集，星点为降维后得到的数据

# 降维前后数据集的对比
plt.plot(remove_mean_x, remove_mean_y, 'o', color='red')
plt.plot([eig_vector[:, 1][0], 0], [eig_vector[:, 1][1], 0],color='blue')
plt.plot([eig_vector[:, 0][0], 0], [eig_vector[:, 0][1], 0], color='blue')
plt.plot(rot_data[:, 0], rot_data[:, 1], '^', color='blue')
plt.plot(new_data[:,0],[1.2]*10,'*',color='black')
plt.show()

原数据集和降维后的数据集

机器学习算法系列（10）主成分分析（PCA）