机器学习中的神经网络（neural networks）算法受到生物界神经系统处理信息的启发，比如大脑处理信息的方式。跟人类一样，神经网络的训练也是一个学习的过程，通过大量的学习，神经网络能够完成特定的任务，比如图像分类识别、疾病预测判断等等。在这篇文章里将简单介绍神经元工作原理和神经网络模型，重点在于理解反向传导算法（BP）中参数的更新过程，并用一个实例解释了BP算法。

本文目录

神经网络
- 理解神经元的工作原理
- 简单神经元模型
- 神经网络模型
- 多层神经网络
反向传导（BP）算法思路
- 定义损失函数
- 随机初始化参数
- 计算残差
BP算法的一次实例更新迭代
- 第一步：前馈传导
- 第二步：反向传导
参考文献

神经网络

理解神经元的工作原理

“神经网络”一词起源于早先模拟（mimic）人类大脑的研究中，而发展到今天的“神经网络”早就已经是一个庞大的交叉学科领域，当然本文讨论的范围在机器学习与神经网络交叉的部分。在进行正式讨论之前，我们有必要先了解一些神经网络的前世今生。

关于神经网络最广泛的定义是

神经网络是由具有适应性的简单单元组成的广泛并且并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应（Kohonen，1988）

从生物学的角度，大脑是人体的最高指挥中心，人的听觉、嗅觉、味觉、触觉、视觉等等感官感受都是通过神经网络来接收、传递、处理的。

神经网络的基本单元是神经元（neuron），神经元的基本组成有细胞核（cell）、树突（dendrite）、轴突（axon）、轴突末梢（axon terminal）。神经元有接收、处理、传递信息的功能。

典型的神经元结构1

当树突从其他神经元接收化学物质(多巴胺、乙酰胆碱)，神经元会变得“兴奋”，于是通过轴突将信息传递给另外的神经元，化学物质在树突与轴突的传递形成电流，如果两个神经元之间的电位差别超过“阈值”，那么它便会被“激活”，这就是神经元的基本工作模式。

在人类的大脑中约有860亿计个神经元，$10^{14}$到$10^{15}$个突触（synapse），正是这些简单的神经元组合可以完成各类复杂工作，于是成就了地球上最智慧的生物——人类。

简单神经元模型

回到机器学习，首先，我们从最简单的神经元模型讲起，也就是神经网络中仅仅只有一个神经元（single neuron）的情形，如图示

一个简单的神经元模型

在上面这个模型中，神经元收到来自其他来自3个神经元（$x_i,i=1,…,3$）的信息，即输入（input），这些输入通过带权重（weights）（$w_j,j=0,1,…,3$）的连接进行传递，对线性组合（$w\cdot x$）的传递汇总，进行激活（activation）处理之后再与当前神经元的阈值进行比较，如果大于阈值，那么该神经元则被激活。注意，这里我们通常将$x_0$和$w_0$均取为1，即把$w_0$当做偏置项（bias）。

将上述过程与生物学的神经元类比，蓝色的圈表示突触，桔色的圈表示细胞核，蓝色与桔色的圈之间的连接表示树突，激活之后的计算结果就好比电位差，只有存在电位差，神经元才有可能会被激活。

典型的神经元结构2

我们通常选择sigmoid函数作为激活函数$f(·)$（activation function）

$f(w,x)=\frac{1}{1+e^{-w^Tx}}$

细心的读者可能会有疑惑，前面说好的“阈值比较”过程去哪里了？不是还有一个判断的过程吗？其实，神经元模型中的激活函数便完成了这个任务，观察sigmoid函数

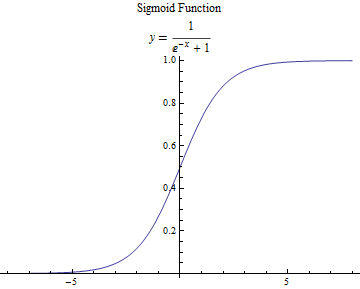
Sigmoid函数

可以看出，线性组合经过sigmoid函数处理，输出值被映射到$(0,1)$的范围内，所以我们可以在此范围灵活地设置阈值以决定神经元是否被激活。“1”对应于激活，“0”对应于抑制。把许多个这样的神经元模型按照一定的结构联系起来，就得到了神经网络。除了sigmoid函数可以作为激活函数，常用的激活函数还有双曲正切函数（tanh）、 ReLU（Rectified Linear Unit）、Maxout等，这里就不详细展开。

神经网络模型

像这样只有输入层和输出层两层的神经元模型也被叫做感知机，感知机能够实现简单的与、或、非逻辑运算，除此之外，感知机学习能力非常有限，对于线性不可分的问题束手无策。

讲到这里，有必要插播一段神经网络研究的历史，神经网络的发展可谓一波三折

首次尝试：1943年McCulloch和Pitts基于神经学奠定了神经网络的基础，拥有单个神经元的神经网络又被称为是“M-P神经元模型”，M-P神经元模型能够解决简单的逻辑问题。除此之外，还有两队人马也加入到了神经网络的研究队伍，分别是IBM和 (Farley and Clark, 1954; Rochester, Holland, Haibit and Duda, 1956)等人。

百家争鸣：神经网络在多个领域发扬光大，如心理学、工程行业。1958年Rosenblatt设计并发展了感知机，使它能够进行简单图像识别，在当时引起了极大轰动。

十年停顿：1969年Minsky和Papert写了一本名为《感知机》的书，书中详细论证了单层感知机无法解决非线性问题，而多层神经网络的训练算法则看不到希望，这一悲观情绪直接导致了神经网络研究的十年停顿，研究经费大幅缩减。

“…our intuitive judgment that the extension (to multilayer systems) is sterile”

“···我们最先对多层神经网络系统的判断是徒劳的”

第二春：1986年Rumelhar和Hinton等人提出了反向传播（Backpropagation，BP）算法，解决了两层神经网络所需要的复杂计算量问题，从而带动了业界使用两层神经网络研究的热潮。

再陷低谷：20世纪90年代中期，Vapnik提出了支持向量机方法，由于不需要调参、全局最优、高效，并在比赛中表现非常好，支持向量机的出现打败神经网络，神经网络再陷低谷。

横空出世：2006年Hinton在《科学》发表论文，提出“深度学习”的概念。2012年，Hinton和他的两个学生在ImageNet图像分类比赛中借助深度学习一举夺魁，深度学习横空出世，谁与争锋！

多层神经网络

神经网络最左边的一层叫做输入层（input layer），最右边的叫做输出层（output layer），中间的所有节点则称为隐藏层（hidden layer）。一般神经网络越复杂，它的隐藏层数则越多，理论上能够胜任的任务也就越复杂。上面的神经网络中，一共有三个输入单元（最下方的偏置项不算），三个隐藏单元和一个输出单元，它是一个回归模型（regression model）。

为了更好地描述神经网络，我们引入三个参数，系数$W_{ij}^{(l)}$表示第$l$层的$j$个单元与第$(l+1)$层第$i$单元的权重，系数$b_i^{(l)}$表示第$l$层第$i$单元的偏置项（注意，偏置项的权重取1），$a_i^{(l)}$表示$l$层第$i$个单元的激活值。

当神经网络得到输入$x_n$，$n$个输入由带权重的连接分别传递到下一层的各个节点，下一层节点将上一层传递下来的数值汇总传入激活函数$f(·)$，神经网络的参数计算过程如下

$a_1^{(2)}=f(W_{11}^{(1)}x_1+W_{12}^{(1)}x_2+W_{13}^{(1)}x_3+b_1^{(1)})\\ a_2^{(2)}=f(W_{21}^{(1)}x_1+W_{22}^{(1)}x_2+W_{23}^{(1)}x_3+b_2^{(1)})\\ a_3^{(2)}=f(W_{31}^{(1)}x_1+W_{32}^{(1)}x_2+W_{33}^{(1)}x_3+b_3^{(1)})\\ h(W,x)=a_1^{3}=f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+W_{13}^{(2)}a_3^{(2)}+b_1^{(2)})$

（注：系数$W_{ij}^{(l)}$表示第$l$层的$j$个单元与第$(l+1)$层第$i$单元的权重）

我们可以简洁一点表示，令

\begin{equation}\begin{split}
z^{(l+1)} = W^{(l)}x + b^{(l)} \
a^{(l+1)} = f(z^{(l+1)})
\end{split}\end{equation}

不考虑偏置项，拥有三个输入单元，三个隐藏单元和一个输出单元的神经网络涉及到12（3×3+3×1）个参数。

考虑该神经网络数值计算过程，像这样给定输入和参数，数值计算一层一层往前推进然后得到一个输出，没有反馈，没有循环的神经网络，我们也给它取了一个名字，前馈神经网络（feedforward neural network）。

实际上，神经网络模型还可以有多个隐藏层，每个隐藏层又可以设定多个参数；神经网络的输出也可以多个，如果具有多个输出，那么神经网络模型任务就由回归（一个输出）变成分类（多个输出）了。理论上神经网络越复杂，参数越多，它能够完成的任务就更复杂。比如2015年微软亚洲研究院在ImageNet计算机识别挑战赛中使用了深达百层的神经网络，比以往成功的神经网络层数多了5倍以上，系统错误率低至3.57%。

反向传导（BP）算法思路

反向传导算法（Backpropagation Algorithm，简称BP算法）是优化神经网络参数迭代的主要算法，BP算法的思路是

前馈传导运算，得到各输出层的输出；

从输出层反推进行反向传导计算，利用梯度下降算法更新参数

在进行反向传导算法推导之前，我们有必要了解几个重要的概念，比如定义损失函数，在参数初始化上要保证随机性，以及最重要的是理解残差的概念。

神经网络的参数众多，而优化神经网络参数用到的批量梯度下降算法中主要的计算又是众多的求偏导计算，所以在进行反向求导时一定要明白参数之间的联系。

定义损失函数

进行优化之前，要定义优化的目标是谁，即目标函数。对于单个样本，定义损失函数为

$J(W,b;x,y)=\frac{1}{2} {||h(W,b,x)-y||}^2$

那么对于整个样本集，损失函数可以定义为

$J(W,b)= \frac{1}{m} \sum J(W,b;x,y) + \frac{\lambda}{2} \sum W^2$

上式中的第一项为平方差项，第二项为正则化项，目的是为了防止过拟合。我们的目标是针对参数$W$和$b$来求$J(W,b)$的最小值。

随机初始化参数

为了求解神经网络，我们需要将参数初始化为一个很小的，接近零的随机数，然后对目标函数使用优化算法。注意，如果所有的参数都是相同的，那么所有的隐藏单元都会得到相同的值，如此一来便失去了优化的意义，随机初始化就是要消除它。通常，我们可以让随机参数服从一个很小的正态分布。

计算残差

残差在反向传导算法中是一个非常非常非常重要，而且有点点难理解的概念！！！

本文中残差的定义来自斯坦福的教程，原教程的公式推导我觉得有点太“详细”了，经常是看到公式后面忘了字母的定义是什么，所以我在此基础上做了简化，希望能够方便理解。

在这之前，务必记住以下两个重要定义

$z^{(l+1)} = W^{(l)}x + b^{(l)}$

我们定义残差为

\begin{equation}\begin{split}
\delta_i^{(nl)} &= \frac {\partial} {\partial{z_i^{(nl)}}} \frac{1}{2} (y_i - a_j^{(nl)})^2 \
&=\frac {\partial} {\partial{z_i^{(nl)}}} \frac{1}{2} (y_i - f(z_j^{(nl)}))^2 \
& =-(y_i-f(z_i^{(nl)}))\cdot f’(z_i^{(nl)})\
& =-(y_i-a_i^{(nl)}) \cdot f’(z_i^{(nl)})\
\label{residual0}
\end{split}\end{equation}

需要注意的是，残差中求偏导的对象是$z_i^{(nl)}$，至于为什么是$z_i^{(nl)}$而不是权重系数，下面会具体说明。

为什么是$z_i^{(nl)}$?

式$\eqref{residual0}$给出了$nl$层，也就是输出层向隐藏层的残差，那么考虑一个只有一个隐藏层的神经网络，再考虑向输入层推进呢？也就是求解$\delta_i^{(nl-1)}$，有

\begin{equation}\begin{split}
\delta_i^{(nl-1)} &= \frac {\partial} {\partial{z_i^{(nl-1)}}} \frac{1}{2} \sum (y_i - a_j^{(nl)})^2 \
&=\sum \frac {\partial} {\partial{z_i^{(nl-1)}}} \frac{1}{2} (y_i - f(z_j^{(nl)}))^2 \
& =\sum -(y_i-f(z_i^{(nl)}))\cdot f’(z_j^{(nl)}) \cdot \frac{\partial z_j^{(nl)}}{\partial z_j^{(nl-1)}}\
& =\sum \delta_j^{(nl)} \frac{\partial z_j^{(nl)}} {\partial z_j^{(nl-1)}}\
& =(\sum \delta_j^{(nl)} W^{nl-1})f’(z_i^{(nl-1)})\
\label{residual1}
\end{split}\end{equation}

这下就终于明白了为什么残差中求偏导的对象是$z_i^{(nl)}$了，因为$z_i^{(nl)}=W^{(nl)}x+b$，神经网络中各个层的权重参数众多，所以这样一来只需要对$z_i^{(nl)}$再求一次偏导，便可以得到想要的权重系数的偏导数。

BP算法的一次实例更新迭代

第一步：前馈传导

如下图，考虑一个神经网络，该神经网络一共有三层，其中有一个隐藏层，两个输入单元，两个隐藏层单元，两个输出单元，外加两个取值为1的偏置项。

以隐藏层第一个激活值$a_1^{(2)}$计算为例（神经网络选择sigmoid函数作为激活函数），连接线上的数字为随机初始化的权重参数，输入节点经加权汇总之后汇入隐藏层。计算方法如下

$a_1^{(3)}=f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+b_1^{(2)})$ $a_2^{(3)}=f(W_{21}^{(2)}a_1^{(2)}+W_{22}^{(2)}a_2^{(2)}+b_1^{(2)})$

前馈传导

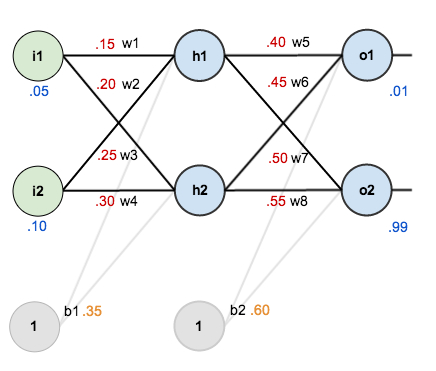
经过前馈传导运算，神经网络最终得到两个输出，分别是0.7513和0.7729。假设真实标签为[0.01, 0.99]，输出和真实标签有误差，需要对其进行优化。

第二步：反向传导

计算总误差，总的误差

$E_T = \frac{1}{2}\sum (y_i - a^{(nl)})^2, a^{(nl)}表示输出层$

所以

$E_T = \frac{1}{2}(0.01-0.7513)^2+\frac{1}{2}(0.99-0.7729)^2 = 0.298$

输出层→隐藏层的权值更新$W_{11}^{(2)}$

考虑$W_{11}^{(2)}$对整体误差的影响，是一个链式求导的过程。

有

$\frac {\partial{E_T}} {\partial{z_{11}^{(3)}}} =\frac {\partial{E_T}} {\partial{a_1^{(3)}}} \frac{\partial{a_1^{(3)}}}{\partial{z_{11}^{(3)}}}$

其中

$z_{11}^{(3)} = f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+b_1^{(2)})$

由式$\eqref{residual0}$，以及sigmoid函数的求导法则，可得

$\delta_1^{3}=-(0.01-0.7513)*0.7513*(1-0.7513)=0.1385$

因为需要更新的权值是$W{11}^{(2)}$，所以再对$z{11}^{(3)}$求$W{11}^{(2)}$偏导即可。假定学习率为0.5，那么$W{11}^{(2)}$更新如下

$W_{11}^{(2)} := W_{11}^{(2)} - \eta \cdot \delta_1^{3} \cdot a_1^{(2)}$

即

$W_{11}^{(2)} := 0.4 -0.5*0.1385*0.5932=0.3589$

同理，我们也可以求得$\delta2^{3}$，并更新相应的权值$W{2j}^{(2)}$，计算过程可以参照$W_{11}^{(2)}$的更新

$\delta_2^{3}= -(0.99-0.7729)*0.7529*(1-0.7529)=-0.0381$

隐藏层→输入层权值更新$ W_{11}^{(1)} $

然而仅仅更新一层的参数是不够的，既然是反向传导，参数的更新便是从右至左的过程，如果要更新输入层至隐藏层之间的参数，又该如何计算呢？如下图，$W_{11}^{1}$的权值（0.15）影响到了两个输出

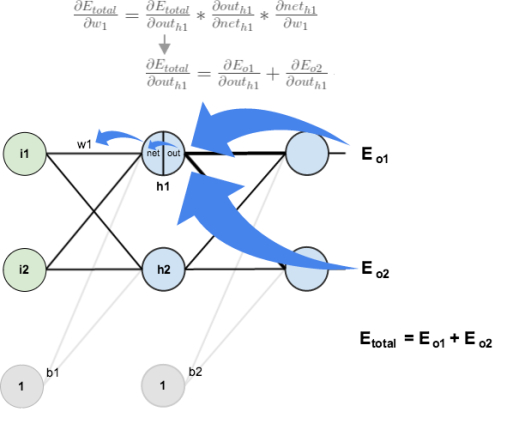
$W{11}^{(1)}$影响到$a_1^{(2)}$的输出，而$a_1^{(2)}$接受来自两个输出$a_1^{(3)}$和$a_2^{(3)}$的误差，所以我们先将偏导数进行到$a_1^{(2)}$，实际上是求解$\sum \delta_j^{(3)} W{ij}^{2}$

\begin{split}
\sum \deltaj^{(3)} W{ij}^{(2)} &= \frac {\partial{E_T}} {\partial{a_1^{(3)}}} \frac{\partial{a_1^{(3)}}}{\partial {a_1^{(2)}}} + \frac {\partial{E_T}} {\partial{a_2^{(3)}}} \frac{\partial{a_2^{(3)}}}{\partial {a_1^{(2)}}} \
&=0.13850.4+(-0.0381)0.5 \
&=0.0538+(-0.0190)\&=0.0348 \
\end{split}

至此，来自两个输出的权值影响就全部汇集到了$a1^{(2)}$。接下来，我们只需要考虑$W{11}^{(1)}$对$a_1^{(2)}$的影响了，这就变得简单多啦！由式$\eqref{residual1}$可得

$f'(z_1^{2}) = 0.5932*(1-0.5932) = 0.2413$

\begin{equation}\begin{split}
\delta1^{(2)} = (\sum \delta_j^{(3)} W{ij}^{(2)}) \cdot f’(z1^{2})\
\label{key}
\end{split}\end{equation}
故$ W{11}^{(1)} $权值更新如下：

$W_{11}^{(1)} := W_{11}^{(1)} - \eta \cdot \delta_1^{(2)} \cdot a_1^{(1)} = 0.1498$ $W_{11}^{(1)} := 0.15 - 0.5 * 0.0348 * 0.2413 * 0.05 = 0.1498$

反向传导最关键的地方在于残差的数值传递，即式$\eqref{key}$，一定要正确理解$\delta_1^{(2)}$与$\delta_j^{(3)}$之间是如何联系起来的！神经网络中的其他参数也可以按照同样的方法进行更新，本文不再赘述。

本文中给出的例子有两个输出，故数值传递比只有一个输出的要更复杂，如果只有一个输出的话，那我们计算$\frac {\partial{E_T}} {\partial {a_1^{(2)}}}$就不用考虑$a_2^{(3)}$的影响

其实这样理解起来挺麻烦的，我们换一个角度看看

$\frac {\partial {a_1^{(2)}}}{\partial W_{11}^{(1)}}=0.5932*(1-0.5932)*0.05=0.0120$ $\frac {\partial{E_T}}{\partial W_{11}^{(1)}} = 0.0348*0.0120=0.0004$

再应用梯度下降算法，$ W_{11}^{(1)} $权值更新如下：

$W_{11}^{(1)} := 0.15 - 0.5 * 0.0004 = 0.1498$

跟上面的方法得出的结果也是一样的，这里并不是说从残差的角度去计算就不好，而是从一个平时我们习惯的视角去更新参数能够加深理解。

参考文献

反向传播算法Python代码 | 我爱自然语言处理
神经网络 - Ufldl
神經元》. 2016. 维基百科，自由的百科全书
微软实现深层神经网络重大技术突破 - 微软亚洲研究院
CS231n Convolutional Neural Networks for Visual Recognition
Neural Networks
《机器学习》. 周志华
《统计学习方法》. 李航
《The Elements of Statistical Learning》Jerome H. Friedman, Robert Tibshirani, and Trevor Hastie
A Step by Step Backpropagation Example – Matt Mazur