机器学习算法系列（9）k均值

发表于 | 更新于 | 分类于 | 阅读次数：

在用户增长分析过程中有时除了需要预测用户的行为，还需要把用户细分为差异比较大的群体，然后针对不同的群体采取相应的运营手段，即用户分群。在机器学习的算法中有一个专门的领域——聚类算法，聚类是一种了解数据内在结构的方法，它通过将数据集中的样本划分为若干不相交的子集，每个子集称为一个“簇”（cluster）。如何定义簇以及簇的数量则完全人工自行决定。在先前的文章中涉及到的算法都是监督学习，现在我们开始接触到机器学习中第一个无监督学习算法——k-均值。不同于以往的数据集，无监督学习所用到的数据集都是没有标签的，也就是事先并不知道数据的内在性质及规律。

k-均值的最终目的是最小化平方误差：

一、k-means基本思路

k-均值算法的基本思路：

  1. 随机生成k个随机质心
  2. 计算样本值到质心之间的欧式距离，将样本点划分到距离最近的质心
  3. 重新更新各个簇的质心位置
  4. 重复2-3步，直到质心位置不再变化
  5. 得出输出结果

二、基于Python的k均值算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
from numpy import *
# 导入文件
file_name = "E:/Python/mla/Ch10/testSet.txt"
def load_data(file_name):
    data_mat = []
    fr = open(file_name)
    for line in fr.readlines():
        # 将文本文档的每一行转换成浮点型并添加到矩阵中
        current_line = line.strip().split('\t')
        data_mat.append([float(current_line[0]), float(current_line[1])])
        dataset = mat(data_mat)
    return dataset
dataset = load_data(file_name)
1
2
3
# 计算向量间欧几里得距离
def cal_dist(vec_a, vec_b):
    return sqrt(sum(power(vec_a - vec_b, 2)))
1
2
3
4
5
6
7
8
9
# 生成k个随机质心（centroids）
def rand_centroid(dataset, k):
    n = shape(dataset)[1]
    centroids = mat(zeros((k, n)))
    for j in range(n):
        min_j = min(dataset[:, j])
        range_j = float(max(dataset[:, j]) - min_j)
        centroids[:, j] = min_j + range_j * random.rand(k, 1)
    return centroids
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# k均值聚类算法
def k_means(dataset, k):
    m = shape(dataset)[0] # 获取数据的行数m
    # 簇分配结果矩阵'cluster'包含两列：
    # 第一列记录簇索引值，第二列存储误差
    cluster = mat(zeros((m, 2)))
    centroids = rand_centroid(dataset, k)
    # 创建一个标志变量'cluster_changed'
    cluster_changed = True
    while cluster_changed:
        cluster_changed = False
        for i in range(m):
            min_dist = inf
            min_index = -1
            # 分别计算'dataset'中第i个点与k个质心之间的欧几里得距离，
            # 并将距离最小的质心的索引赋给簇分配结果
            for j in range(k):
                dist_i_j = cal_dist(centroids[j, :], dataset[i, :])
                if dist_i_j < min_dist:
                    min_dist = dist_i_j
                    min_index = j
            if cluster[i, 0] != min_index:
                cluster_changed = True
            cluster[i, :] = min_index, min_dist**2
        print(centroids)
        # 更新质心的位置，直到簇分配结果不再改变为止
        for cent in range(k):
            index = cluster[:, 0].A # 簇分配结果中的所有索引
            value = nonzero(index == cent)
            sample_in_cent = dataset[value[0]]
            centroids[cent, :] = mean(sample_in_cent, axis=0) # 按列计算均值
    return centroids, cluster

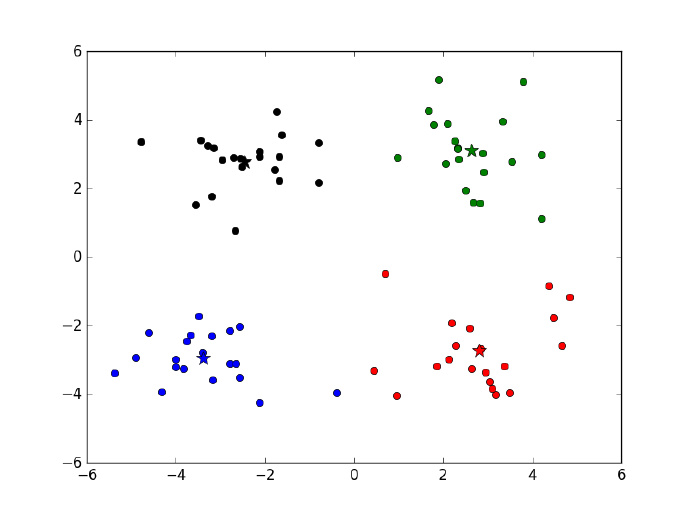
经过四次迭代之后算法收敛，得到4个质心，四个质心以及原始数据的散点图在下图给出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[[ 1.71514331  4.38373482]
 [-2.07697989 -2.34923269]
 [ 1.37232864 -1.69241204]
 [-4.4940993  -0.98212537]]
[[ 1.21336621  3.14825539]
 [-2.98849186 -3.14785829]
 [ 2.8692781  -2.54779119]
 [-3.56936853  0.80979859]]
[[ 1.98283629  3.1465235 ]
 [-3.38237045 -2.9473363 ]
 [ 2.80293085 -2.7315146 ]
 [-2.768021    2.65028438]]
[[ 2.6265299   3.10868015]
 [-3.38237045 -2.9473363 ]
 [ 2.80293085 -2.7315146 ]
 [-2.46154315  2.78737555]]
1
2
3
4
5
6
7
8
9
10
11
def showCluster(dataset, k, centroids, cluster):
    numSamples, dim = dataset.shape
    mark = ['or', 'ob', 'og', 'ok']
    for i in range(numSamples):
        markIndex = int(cluster[i, 0])
        plt.plot(dataset[i, 0], dataset[i, 1], mark[markIndex])
    mark = ['*r', '*b', '*g', '*k']
    # 画出质心
    for i in range(k):
        plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12)
    plt.show()

k均值聚类的结果

三、如何选择合适的K？

与其说为k均值选择合适的聚类数k，倒不如说检验聚类的效果如何，因为k均值是无监督类的分析方法，所以在运用K均值算法的时候比较头疼的是我们事先无法知道最优的聚类个数。假定即使你事先确定了聚类的个数，而实际上也不一定能对应上，并且聚类的结果很大程度上依赖于分析人员喂给聚类模型的变量。在用Spark做k均值聚类时候通常有两个评估指标：

  • 簇内误差平方之和：WSSSE（Within Set Sum of Squared Errors），Scala Spark计算损失的接口，computeCost，根据Spark文档的解释：sum of squared distances of points to their nearest center，即簇内误差平方之和是点距离它所归属的簇中心点的距离平方和，该值越小越好，表明簇类内部的样本距离越接近。
  • 轮廓值(Silhouette score)：是聚类效果好坏的一种评价方式，轮廓系数的值是介于[-1,1]，越趋近于1代表内聚度和分离度都相对较优。轮廓系数的计算公式：$s_i = (b_i – a_i)/max(a_i,b_i)$，其中$a_i$表示簇内的聚集程度，对于第i个元素$x_i$，计算$x_i$与其同一个簇内的所有其他元素距离的平均值；选取$x_i$外的一个簇b，计算$x_i$与b中所有点的平均距离，遍历所有其他簇，找到最近的这个平均距离，记作$b_i$，用于量化簇之间分离度。计算所有x的轮廓系数，求出平均值即为当前聚类的整体轮廓系数。Spark的使用方法见：Clustering - Spark 2.4.0 Documentation

四、讨论

k均值算法最大的优点就是运行速度快，在Spark上对10W条数据190个特征进行聚类分析，不到两分钟就可以跑完，速度还是非常快的，其实最主要的工作还是分析人员不断分析评估各种模型的好坏。但是它的劣势也是很明显的，比如它的区分度不是很好，对于稀疏数据的聚类，大多数的数据都集中在一块，无法剥离出来；到底K取多少需要分析人员不断尝试；另外，聚类分析需要用到什么变量也需要谨慎考虑，在聚类分析中我们应该使用与问题紧密相关的变量做聚类而不是使用所有的变量作为输入。

  • 对异常值敏感，因为在计算各个簇质心位置时，异常点往往会使得结果变得扭曲
  • 在对事物没有一定了解的前提下事先难以确定k值
  • 算法的时间复杂度较高，在处理大数据时是相对可伸缩和有效的，通常需要使用合适规模的样本
  • 只能发现球状簇，对不规则的簇效果一般

解决异常值敏感可采用k中心算法，k中心点算法中，每次迭代后的质点都是从聚类的样本点中选取，而选取的标准就是当该样本点成为新的质点后能提高类簇的聚类质量，使得类簇更紧凑。该算法使用绝对误差标准来定义一个类簇的紧凑程度。另外的优化手段还有凝聚的与分裂的层次聚类。

参考

  1. 腾讯QQ大数据：用户增长分析——用户分群分析
  2. Clustering - Spark 2.4.0 Documentation
------本文结束，欢迎收藏本站、分享、评论或联系作者！------
相关文章
点击查看
赠人玫瑰 手有余香
0%