将来训练上出现偏差,等于…你…你也有责任吧!
从统计学的意义上来说,方差(variance)是衡量数据的离散程度,而偏差(bias)则是反映数据与真实情形的偏离程度。
假设有一个样本$x$,$y$是测试样本的真实标记,$f(x)$是模型根据样本训练得出的预测输出结果,预测输出结果的期望为$\bar{f}(x)$,则有
预测结果在样本集上的分散程度(偏离期望)方差为,
预测输出结果与真实标记的差别称为偏差,
下面这个图可以很好地解释偏差与误差之间的区别,圆圈中间的红点代表数据的真实标记,蓝点表示模型的预测结果。很明显,在高方差情形下,模型的预测结果很分散,反之则很集中;在高偏差情形下,模型预测结果的正确率极低,反之则很高。
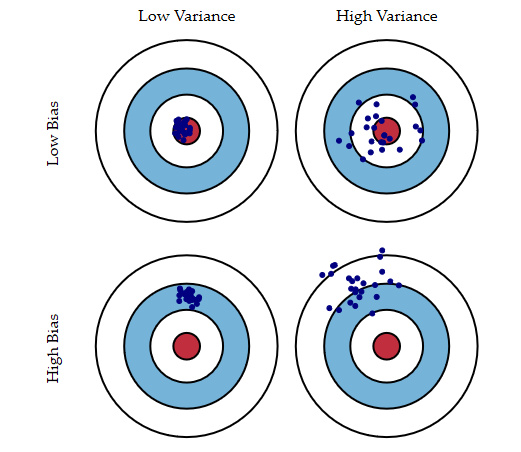
可以说,方差和偏差分别评价了两个不同因素(数据、模型)在机器学习中的表现,也可以这样来理解:方差代表了数据扰动所造成的影响,增大样本容量通常可以减轻数据扰动带来的影响;偏差则刻画了算法或模型的拟合能力,它与数据本身关系不太大,通过特征工程、调节参数、选择模型等手段可以解决偏差问题。随着训练程度的增大,学习器拟合性能越来越强,偏差会越来越小,而数据的任何扰动则会使已经完善的学习器产生较大方差。

