处理不平衡数据——基于UCI人口调查数据集（一）

Like it or not , a bitter truth about data science industry is that self-learning, certification, coursework is not sufficient to get you a job.

本项目github地址：https://github.com/swordspoet/UCI_imbalanced_data

前言

这是一篇关于如何处理美国人口调查不平衡数据集的文章，是基于R来处理的。

学习R语言，如果没有在实际数据集当中去来回操作，说到底还是纸上谈兵。大家还是相信这句话，Talk is cheap, show me the code。个人觉得R语言的学习曲线比较高，当中的东西太多太杂，编码起来特别麻烦，文档方面做得也不如Python那么全面，要想在短时间内在R中做到触类旁通简直艰难。在完成这个小项目的过程中，踩了好多坑，切切实实体会到了R在处理规模数据方面的性能短板，还有教科书提到的数据清洗和工程应用中的数据清洗完全是两回事。写完这篇文章之后，感觉自己的编程能力太渣，代码的编写阅读量还是太少，任重道远~

在实际工程中，有一些极端条件（欺诈检测、癌症诊断、在线广告捕捉）会使得数据集十分不平衡，毕竟干坏事、得绝症的个体在人群中的比例是较小的，这样就导致目标变量的分布可能会呈现极端分布态势，给我们的模型预估带来困难。

做这个项目有什么好处呢？

• 处理不平衡数据是一个技巧性的工作
• 数据的维度高，因此，它可以帮助你理解和克服机器的内存问题
• 提升你的编程、数据分析和机器学习技能

一、描述问题&生成假设

任务要求：给定拥有多个变量的数据集，目标是根据这些变量来建立一个预测收入水平是大于50000还是小于50000的分类模型。

Prediction task is to determine the income level for the person represented by the record. Incomes have been binned at the $50K level to present a binary classification problem, much like the original UCI/ADULT database.

从问题的描述来看，这是一个二分类问题，任务要求目标函数输出的结果只有两种类型，即“是”或者“否”。

在这个项目中我们用到的是来自UCI机器学习的数据集，这是一份美国人口的调查数据，打开数据集，我们会发现列名全部都丢失了，完好的数据集在这里下载训练集、测试集。

一般，我们拿到数据要做的第一件事便是先打开看看，思考数据量有多大？有多少个变量？变量是连续型的还是非连续型的？有没有缺失数据？目标变量在哪里？······

二、探索数据

# 加载包和数据集
# na.string=c()定义多个变量（""   " "  "?"  "NA" NA）为NA

library(data.table)
train <- fread("E:/R/imbalancedata/train.csv",na.string=c(""," ","?","NA",NA)) 
test <- fread("E:/R/imbalancedata/test.csv",na.string=c(""," ","?","NA",NA))

从数据加载之后的情况来看，训练集中有199523个观测值，41个变量，测试集的观测值有99762个，同样也是41个变量。回到我们的目标，我们的目标是要建立预测收入的模型，那么因变量是什么？是收入水平（income_level）。

找到因变量（income_level），训练集和测试集下的income_level变量下只有-50000和+50000两种取值分别对应小于50000和大于50000两种取值。为了方便，将income_level下的取值替换为0（小于50000）和1（大于50000）。

unique(train$income_level)
unique(test$income_level)
[1] "-50000" "+50000"
[1] "-50000"  "50000+."
# 将目标变量取值替换为0,1，ifelse(test,yes,no)
train[,income_level:= ifelse(income_level == "-50000",0,1)] 
test[,income_level:= ifelse(income_level == "-50000",0,1)]

接着，继续查看训练集的正负样本分布情况

round(prop.table(table(train$income_level))*100)
 0  1 
94  6

从返回结果可以看出，原始训练集的正负样本分布非常不均衡，收入水平小于5万的人群占据了94%，大于5万的人群仅仅占了6%（毕竟有钱人还是少！）。这是一个典型的不平衡数据集，正负样本差别太大，很容易对模型的准确性造成误解。例如有98个正例，2个反例，那么只需要建立一个永远返回正例的预测模型就能轻松达到98%的精确度，这样显然是不合理的。

那么如何由这种不平衡数据集学习到一个准确预测收入水平的模型呢？这是主要要解决的难题，在解决这个问题之前需要对数据进行预处理。

三、数据预处理

首先，从数据集介绍的页面可以了解到，变量被分为nominal（名义型）和continuous（连续型）两种类型，即分别对应类别型和数值型。

对数据进行预处理时，我们先将这两种不同的数据类型切分开来分别处理，data.table包可以帮助我们快速简单地完成这个任务。

#数据集介绍的页面已经告诉我们哪些特征为nominal或是continuous
factcols <- c(2:5,7,8:16,20:29,31:38,40,41)
numcols <- setdiff(1:40,factcols)
# lapply的.SD的用法
train[,(factcols) := lapply(.SD, factor), .SDcols = factcols]
train[,(numcols) := lapply(.SD, as.numeric), .SDcols = numcols]
test[,(factcols) := lapply(.SD, factor), .SDcols = factcols]
test[,(numcols) := lapply(.SD, as.numeric), .SDcols = numcols]
# 将训练集和测试集中的类别变量和数值变量分别提取出来
cat_train <- train[,factcols, with=FALSE]
cat_test <- test[,factcols,with=FALSE]
num_train <- train[,numcols,with=FALSE]
num_test <- test[,numcols,with=FALSE]

经过上述的处理，训练集和测试集分别被拆分为类别型和数值型两个部分，一共是4个子数据集，并且在处理的过程中规定了它们的类型是factor还是numeric。

四、数据可视化

单纯查看数据集无法得到直观的感受，“一图胜千言”，图形是最简单直观的办法，下面我们会用到ggplot2和plotly两个强大的绘图包。

library(ggplot2)
library(plotly)
# geom_histogram()直方图
# geom_density()密度图
# aes设定x轴y轴的名称
tr <- function(a){ggplot(data = num_train, aes(x= a, y=..density..)) +
geom_histogram(fill="blue",color="red",alpha = 0.5,bins =100) + geom_density()
ggplotly()
}

tr(num_train$age)
tr(num_train$capital_losses)

以上两个分布图符合我们的常识，年龄分布在0~90岁之间，年龄越大，所占比例越小。

自变量与因变量之间的关系

我们分别考虑训练集中的数值型变量和类别型变量与income_level的关系。

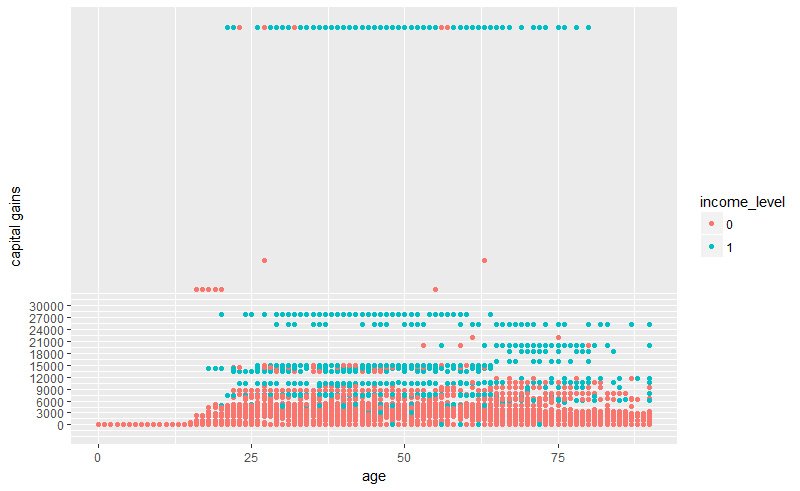
首先看数值型的，数值型训练集num_train下有wage_per_hour、capital_gains、capital_losses、dividend_from_Stocks等等几个变量，我们选取了四个关联程度较大的指标，可以看出，大部分年龄段处于25-65的人收入水平income_level为1（大于50000），他们的小时工资（wage per hour）处在1000美元到4000美元的水平。这个事实进一步强化了我们认为年龄小于20的人收入水平小于50000的假设。

#income_level属于类别型的，被切分到了cat_train中
num_train[,income_level := cat_train$income_level]
ggplot(data=num_train,aes(x = age,
y=wage_per_hour))+geom_point(aes(colour=income_level))+scale_y_continuous("wage per
hour", breaks = seq(0,10000,1000))

股票收益对收入的影响也是比较大的，收入水平大于50000的人群基本上股票分红都超过了30000美元

num_train[,income_level := cat_train$income_level]
ggplot(data=num_train,aes(x = age,y=dividend_from_Stocks))+geom_point(aes(colour=income_level))+
  scale_y_continuous("dividend from stocks", breaks = seq(0,10000,5000))

类似地，我们可以还可以查看capital_gains资本增值和capital_losses资本贬值与收入水平的关系，如下图所示

同样的，我们也可以将分类变量以可视化的形式展现出来，对于类别数据，dodged条形图比一般条形图能展更多的信息。在dodged条形图中，可以发现很多有趣的东西，比如本科毕业生年薪超过5万的人数最多，拥有博士学位的人年薪超过5万和低于5万的比例是相同的，白人年薪超过5万的人群远远多于其他肤色的种族

all_bar <- function(i){
 ggplot(cat_train,aes(x=i,fill=income_level))+geom_bar(position = "dodge",  color="black")+scale_fill_brewer(palette = "Pastel1")+theme(axis.text.x =element_text(angle = 60,hjust = 1,size=10))
}

五、数据清洗

检查遗漏值

数据清洗时数据分析的一个重要步骤，首先检查训练集和测试集中是否有遗漏值

table(is.na(num_train))
table(is.na(num_test))

从反馈的结果来看，FALSE分别等于1396661=199523×7，698334=99762×7，故训练集和测试集中的数值型（num）部分没有一个遗漏值，这是一个不错的消息！而检查类别型（cat）数据时，数据遗漏的情况就比较严重了。

> table(is.na(cat_train))

  FALSE    TRUE 
6367191  416591 
> table(is.na(cat_test))

  FALSE    TRUE 
3183124  208784

删除高度相关变量

变量之间的相关性对模型的准确性存在影响，caret包能够帮助我们检查数值型变量之间的相关性，筛选出高度相关的变量

library(caret)
x <- cor(num_train)
ax <- findCorrelation(x, cutoff=0.7)
num_train <- num_train[,-ax,with=FALSE]
num_test <- num_test[,weeks_worked_in_year := NULL]

筛选的结果显示，weeks_worked_in_year变量与其他变量存在相当高的相关性。这很好理解，因为一年之中工作的时间越长那么相应的工资、回报也会随之上涨，所以要把这个高度相关性的变量剔除掉，这样num_train当中就只剩下7个变量了。

似乎数值型的数据已经处理得差不多了，下面我们来看看类别型的数据cat_train，首先检查每一列数据的遗漏情况

mvtr <- sapply(cat_train, function(x){sum(is.na(x))/length(x)})*100
mvte <- sapply(cat_test, function(x){sum(is.na(x)/length(x))}*100)

mvtr
mvte

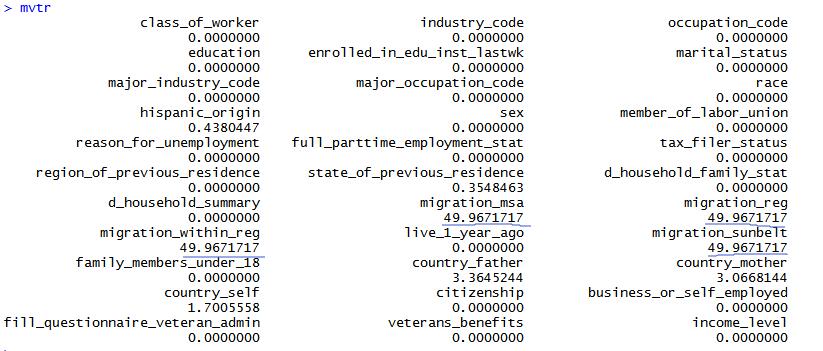
大部分的列情况比较乐观，但是有的列甚至有超过50%的数据遗漏（这有可能是由于采集数据难度所致，特别是人口普查），将遗漏率小于5%的列挑选出来，遗漏率太高的变量剔除掉。

cat_train <- subset(cat_train, select = mvtr < 5 )
cat_test <- subset(cat_test, select = mvte < 5)

#对于挑选出来的遗漏率小于5%的列的遗漏值，比较好的办法是将其标记为“Unavailable”

cat_train <- cat_train[,names(cat_train) := lapply(.SD, as.character),.SDcols = names(cat_train)]

for (i in seq_along(cat_train)) set(cat_train, i=which(is.na(cat_train[[i]])), j=i, value="Unavailable")

cat_train <- cat_train[, names(cat_train) := lapply(.SD,factor), .SDcols = names(cat_train)]

cat_test <- cat_test[, (names(cat_test)) := lapply(.SD, as.character), .SDcols = names(cat_test)]

for (i in seq_along(cat_test)) set(cat_test, i=which(is.na(cat_test[[i]])), j=i, value="Unavailable")

cat_test <- cat_test[, (names(cat_test)) := lapply(.SD, factor), .SDcols = names(cat_test)]

六、数据操作——规范化处理

在前面的分析中，有的类别变量下个别水平出现的频率很低，这样的数据对我们的分析作用不是特别大。在接下来的步骤中，我们的任务是将这些变量下频率低于5%的水平字段设置为”Other”。处理完类别型数据之后，对于数值型数据，各个变量下的水平分布过于稀疏，所以需要将其规范化。

#将cat_train和cat_test中每列下出现频率低于5%的水平设置为“Other”
for(i in names(cat_train)){
  p <- 5/100
  ld <- names(which(prop.table(table(cat_train[[i]])) < p ))
  levels(cat_train[[i]])[levels(cat_train[[i]]) %in% ld] <- "Other"
}

for(i in names(cat_test)){
  p <- 5/100
  ld <- names(which(prop.table(table(cat_test[[i]])) < p ))
  levels(cat_test[[i]])[levels(cat_test[[i]]) %in% ld] <- "Other"
}

#"nlevs"参数：返回每列下维度的个数，测试集和训练集是否匹配

summarizeColumns(cat_train)[,"nlevs"] 
summarizeColumns(cat_test)[,"nlevs"]

num_train[,.N,age][order(age)]
num_train[,.N,wage_per_hour][order(-N)]

#以0，30，90为分隔点，将年龄段划分为三个区段，“young”，“adult”，“old”
num_train[,age:= cut(x = age,breaks = c(0,30,60,90),include.lowest = TRUE,labels = c("young","adult","old"))]
num_train[,age := factor(age)]

num_test[,age:= cut(x = age,breaks = c(0,30,60,90),include.lowest = TRUE,labels = c("young","adult","old"))]
num_test[,age := factor(age)]

#将wage_per_hour，capital_gains，capital_losses，dividend_from_Stocks设置为只有0和大于0两个水平
num_train[,wage_per_hour := ifelse(wage_per_hour == 0,"Zero","MoreThanZero")][,wage_per_hour := as.factor(wage_per_hour)]
num_train[,capital_gains := ifelse(capital_gains == 0,"Zero","MoreThanZero")][,capital_gains := as.factor(capital_gains)]
num_train[,capital_losses := ifelse(capital_losses == 0,"Zero","MoreThanZero")][,capital_losses := as.factor(capital_losses)]
num_train[,dividend_from_Stocks := ifelse(dividend_from_Stocks == 0,"Zero","MoreThanZero")][,dividend_from_Stocks := as.factor(dividend_from_Stocks)]

num_test[,wage_per_hour := ifelse(wage_per_hour == 0,"Zero","MoreThanZero")][,wage_per_hour := as.factor(wage_per_hour)]
num_test[,capital_gains := ifelse(capital_gains == 0,"Zero","MoreThanZero")][,capital_gains := as.factor(capital_gains)]
num_test[,capital_losses := ifelse(capital_losses == 0,"Zero","MoreThanZero")][,capital_losses := as.factor(capital_losses)]
num_test[,dividend_from_Stocks := ifelse(dividend_from_Stocks ==0,"Zero","MoreThanZero")][,dividend_from_Stocks := as.factor(dividend_from_Stocks)]

组合数据

mlr()是R语言中专门应对机器学习问题而开发的包，而在mlr出现之前，R语言中是不存在像Scikit-Learn这样的科学计算工具的。在R语言中使用mlr包只要记住三个步骤即可：

• Create a Task：创建一个任务task
• Make a Learner：给创建的任务选择相应的算法，如分类、聚类等等
• Train Them：然后再训练它！

d_train <- cbind(num_train, cat_train)
d_test <- cbind(num_test, cat_test)

library(mlr)
train.task <- makeClassifTask(data = d_train, target = "income_level")
test.task <- makeClassifTask(data = d_test, target = "income_level")
# Remove constant features from a data set.
# Constant features can lead to errors in some models 
# and obviously provide no information in the training set that can be learned from
train.task <- removeConstantFeatures(train.task)
test.task <- removeConstantFeatures(test.task)

七、处理不平衡数据集

应对不平衡数据集，通常的技巧有上采样(oversampling)、下采样(undersampling)，以及过采样的一种代表性方法SMOTE(Synthetic
Minority Oversampling TEchnique)算法。

• 上采样：即增加一些正例使得正、反例数目接近，然后再进行学习
• 下采样：去除一些反例使得正、反例数目接近，然后进行学习
• SMOTE：SMOTE 是上采样的代表算法，它通过对训练集里的正例进行插值来产生额外的正例，主要思想是通过在一些位置相近的少数类样本中插入新样本来达到平衡的目的
• EasyEnsemble：EasyEnsemble 是下采样的代表性算法，它利用集成学习机制，将样本划分为若干个集合供不同的学习器使用

下采样法的时间开销通常远远小于上采样法，因为前者丢弃了很多反例，使得训练集远小于初始训练集，下采样另外一个可能的缺陷在于
它可能会导致信息的丢失。上采样法增加了很多正例，训练集的大小大于初始训练集，训练时间开销变大，而且容易导致过拟合。

更多关于SMOTE采样方法，Chawla 的这篇文章有详细的说明。

train_under <- undersample(train.task, rate = 0.1)
table(getTaskTargets(train_under))

train_over <- oversample(train.task, rate = 15)
table(getTaskTargets(train_over))

system.time(train_smote <- smote(train.task, rate = 15, nn=3))

八、训练Naive Bayesian分类器

naive_learner <- makeLearner("classif.naiveBayes", predict.type = "response")
naive_learner$par.vals <- list(laplace = 1)

folds <- makeResampleDesc("CV", iters = 10, stratify = TRUE)

fun_cv <- function(a){
  crv_val <- resample(naive_learner,a,folds,measures = list(acc,tpr,tnr,fpr,fp,fn))
  crv_val$aggr
}

模型评估

# 训练结果，从训练结果得知，对不平衡数据集采取不同的采样
# 方法得出的结果截然不同
fun_cv(train.task)
# Result: 
# acc.test.mean=0.732,tpr.test.mean=0.721,tnr.test.mean=0.896,
# fpr.test.mean=0.104,fp.test.mean= 129,fn.test.mean=5.21e+03
fun_cv(train_under)
# Result:
# acc.test.mean=0.785,tpr.test.mean=0.656,tnr.test.mean=0.914,
# fpr.test.mean=0.0856,fp.test.mean=1.59e+03,fn.test.mean=6.44e+03
fun_cv(train_over)
# Result: acc.test.mean=0.785,tpr.test.mean=0.656,
# tnr.test.mean=0.914,fpr.test.mean=0.0856,fp.test.mean=1.59e+03,fn.test.mean=6.44e+03
fun_cv(train_smote)
# Result: acc.test.mean=0.896,tpr.test.mean=0.842,tnr.test.mean=0.951,
# fpr.test.mean=0.0488,fp.test.mean= 906,fn.test.mean=2.96e+03

nB_model <- train(naive_learner, train_smote)
nB_predict <- predict(nB_model, test.task)

nB_prediction <- nB_predict$data$response
dCM <- confusionMatrix(d_test$income_level,nB_prediction)
precision <- dCM$byClass['Pos Pred Value']
recall <- dCM$byClass['Sensitivity']
Specificity <- dCM$byClass['Specificity']
# 准确率precision ：0.844
# 召回率recall 0.985
# 真阴性率Specificity：0.254

# F值
f_measure <- 2*((precision*recall)/(precision+recall))
f_measure
# Pos Pred Value 
     0.9089276

由实验结果，学习得到的模型达到0.844的准确率和0.985的召回率，而真反例仅仅为0.254。也就是说明训练得到的模型在预测收入低于50000的时候表现还行，而一旦要预测收入大于50000的时候表现就不佳了，测试集中仅仅只有25.4%的负样本被检测出来了。这样的结果不太令人满意，在接下来的文章中我们继续探讨其他模型是不是有更好的效果。

（未完）

参考文献

1. Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of artificial intelligence research, 2002, 16: 321-357.
2. Chawla N V. Data mining for imbalanced datasets: An overview of Data mining and knowledge discovery handbook. Springer US, 2005: 853-867.
3. This Machine Learning Project on Imbalanced Data Can Add Value to Your Resume