逻辑斯蒂回归(Logistic regression,以下简称“LR”)和支持向量机(Support vector machine,以下简称“SVM”)都是机器学习中应用十分广泛的分类算法,两种算法在分类任务中的表现各有千秋,笔者在学习完LR和SVM后觉得有必要对这两种算法进行比较。参考论文及网络内容后,本文主要从思路、参数估计、样本分布下实验效果几个方面来进行对比。(个人笔记,如有纰漏,不吝赐教!)
1. 两种算法的思路比较
在之前的一篇文章机器学习算法系列(3)Logistic Regression | Thinking Realm中我们提到 LR 本质上是一类广义线性模型(GLM),只是因为一般的线性模型无法较好地处理分类预测问题。LR 的目的在于最大化数据接近于真实标记的概率,实际上是概率模型的手段;数据越远离分隔超平面,LR的效果就越好。我们还可以根据实际情形来调整划分门槛(threshold),从而得到不同的分类结果。
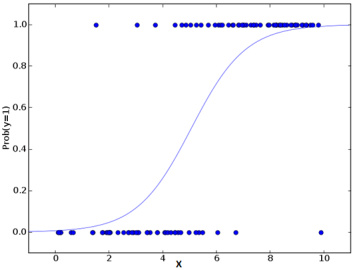
SVM 试图找出一个超平面,模型优化的目标是使距离它最近的点到它的距离之和最大,通常通过核技巧使线性不可分的数据集映射到新的特征空间。
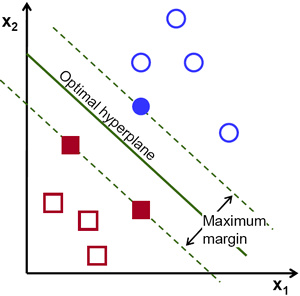
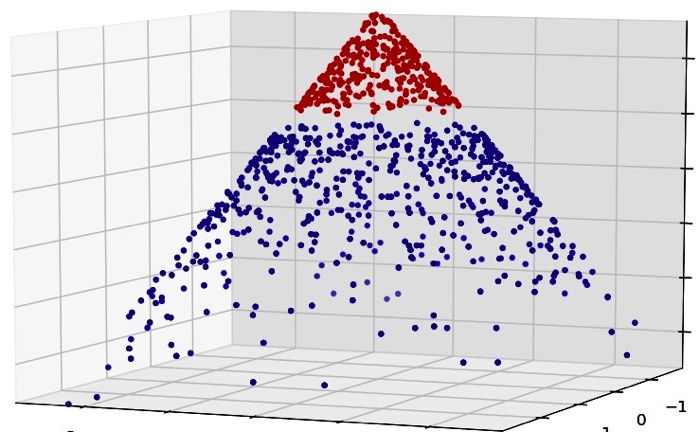
2. 参数估计方式
LR 实际上是对线性回归模型的预测结果取逼近真实标记的对数几率(log odds),即反映了预测结果接近真实的可能性,可能性当然是越大越好。用最大似然估计法来估计参数 $w$,它是一种参数估计方法,LR的损失函数形式如下
\begin{equation}
J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh_w(x^{(i)})+(1-y^{(i)})log(1-h_w(x^{(i)}))]
\end{equation}
与 LR 不同,SVM 的目标函数包含约束条件,它是一种非参数估计方法,故采用拉格朗日乘子法求解参数,得到损失函数如下
\begin{equation}
L(w,b,\alpha)=\frac{1}{2}{||w||}^2-\sum_{i=1}^m{\alpha_i(1-y_i(w^Tx_i+b))} \label{lagrangefunction}
\end{equation}
其二,两者用到的优化方法也不一样,LR 用到的优化方法有梯度下降算法(GD)和随机梯度下降算法(SGD),而 SVM 是通过序列最小最优算法(SMO)求解参数。(个人感觉理解 SMO 的难度远远大于 SGD)
对比 LR 和 SVM 的损失函数,两者都可以添加正则化项,SVM 的损失函数像是一个合页,故名为合页损失函数。合页损失函数实际上是0-1损失函数的优化版本,对比0-1损失函数,由下图,合页损失函数不仅要求分类正确,而且确信度够高时损失才会为0,所以,合页损失函数对学习有更高的要求。
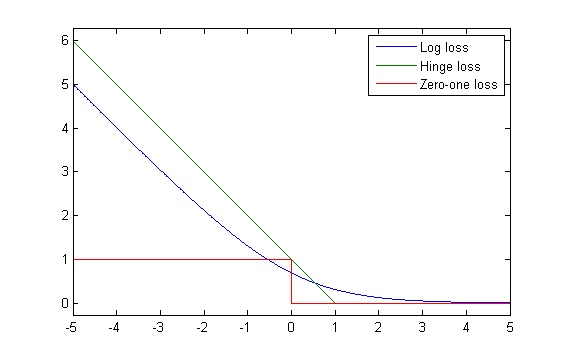
3. 实验效果比较
以下内容选自一篇用统计仿真方法比较 SVM 和 LR 的论文,关于 SVM 和 LR 的基础知识可以参考笔者之前的文章。下面是针对论文的部分实验结果讲解
3.1 单变量分布情形
- 一般情况下,多项式核 SVM 的误分类率比较高。另外,LR和线性核、径向基核、sigmoid 核 SVM 模型的表现差不多。当样本容量发生变化,sigmoid 核和多项式核比其他核的误分类率更低
- 样本数据不平衡的时候,LR 比 SVM 更胜一筹
- 在样本服从指数分布情形下,除了多项式核,SVM 跟 LR 表现得一样好,样本容量分布不平衡时,LR 比 SVM 模型表现更好;样本服从正态分布、泊松分布时,不推荐多项式核 SVM
这里是实验结果

3.2 混合分布情形
正态-泊松混合分布:SVM 比 LR 表现要好,特别是 d 很小
柯西-正态混合分布:SVM 模型比 LR 表现更佳
当基于单个变量来预测新的观测值属于哪个类别,SVM模型比LR更加合适。然而,SVM在泊松分布、指数分布和正态分布样本中,我们不推荐多项式核SVM模型,因为它的误分类率实在是太高了。考虑到多变量和多分布混合情形,当数据中存在高相关部分时,SVM比LR表现得更好。
4. 小结
- 视具体情况而定,优先考虑 LR,LR 简单、快速、易于解释,实在不行再考虑 SVM
- LR 得到的是一个可以解释决策置信度的概率,它的目标函数没有约束条件,并且十分平滑,而 SVM 不是基于概率的,它的目标函数有约束条件,因此两者的参数估计手段完全不同
- SVM 的泛化性能佳,SVM 不会对有足够置信度的点支付一个惩罚,所以假设一个数据集已经被 SVM 求解,那么将一类点删除或是增加并不会改变 SVM 的求解结果
- LR 在不平衡数据集中的表现优于 SVM,SVM 在样本服从混合分布情形下表现优于 LR
- LR 和 SVM 对数据的敏感程度不同,LR 中每一个数据点都会影响到效果,而 SVM 的性能并不依赖于整体数据
- SVM 需要考虑数据的几何距离和函数距离,所以处理时需要对数据做归一化处理,而 LR 则不需要
5. 讨论
@梁斌penny: svm核方法升维,使得在高维上的线性切割,投射到实际空间就变为非线性的切割;lr通过增加大量非线性特征,使得获得非线性切割能力;深度学习通过二层以上神经网络获得非线性切割。核心都需要有非线性识别能力
@phunter_lau: 其实解决问题最有效的模型是LR和SVM,然后是决策树系列xgboost,对于特定结构化数据才是深度学习,最近火是因为一些之前不能做的大规模结构化数据问题能搞了,这不能说其他模型就没用了对吧
豆豆叶:Linear SVM不直接依赖数据分布,分类平面不受一类点影响;LR则受所有数据点的影响,如果数据不同类别strongly unbalance一般需要先对数据做balancing。Linear SVM 和 LR 有什么异同?
6. 推荐阅读
- http://www.kurims.kyoto-u.ac.jp/EMIS/journals/RCE/V35/v35n2a03.pdf
- www.cs.toronto.edu/~kswersky/wp-content/uploads/svm_vs_lr
- http://www.edvancer.in/logistic-regression-vs-decision-trees-vs-svm-part2/
- 相关讨论:Linear SVM 和 LR 有什么异同?

