机器学习算法系列（6）支持向量机（三）

发表于 | 更新于 | 分类于 | 阅读次数：

前两篇笔记主要记录了在线性可分、线性不可分和非线性可分三种情形下，如何将支持向量机的原始优化问题转化为只有一个参数的对偶问题，对偶问题的求解实现没有记录，这篇笔记讲到的序列最小最优算法（SMO）就是一种高效实现支持向量机学习的算法。

由上一篇笔记，凸二次规划的对偶问题

1. SMO 算法基本思路

不同于之前解决二次规划问题所采取的手段，SMO 选择在每一步解决一个最小可能的优化问题，通过求解子问题来逼近原始问题，这可以大大提高整个算法的计算速度，是一种启发式的方法。SMO 与提升树中的前向分步算法或者ALS（交替最小二乘法）的思路殊途同归，它们都是通过不断解决小问题来逼近最优解。

SMO 的优势：

  1. can be done analytically
  2. 不需要额外的矩阵存储空间
  3. SMO = analytic method + heuristic（启发式）

由上述对偶问题，假设先固定除$\alpha_1,\alpha_2$之外的所有其他变量，于是对偶问题的子问题可以等价写为

由对偶问题的约束条件$\sum_{i=1}^{N}\alpha_iy_i=0$，得：

左右两边同乘一个$y_1$，得：

因为${y_1}^2$恒为1，显然：

我们将$\alpha_1$代入子问题，从而消去$\alpha_1$。也就是说，对偶问题两个变量中只有一个是自由变量，实际上是单变量的优化问题，这样问题就更加简化了！

2. 两个变量的凸二次规划问题求解

通过变换，我们将子问题变成了只有$\alpha_2$的单变量优化问题。如何求解$\alpha_2$？考虑两种情形

（1）考虑$y_1*y_2$的两种不同情形

图1

图2

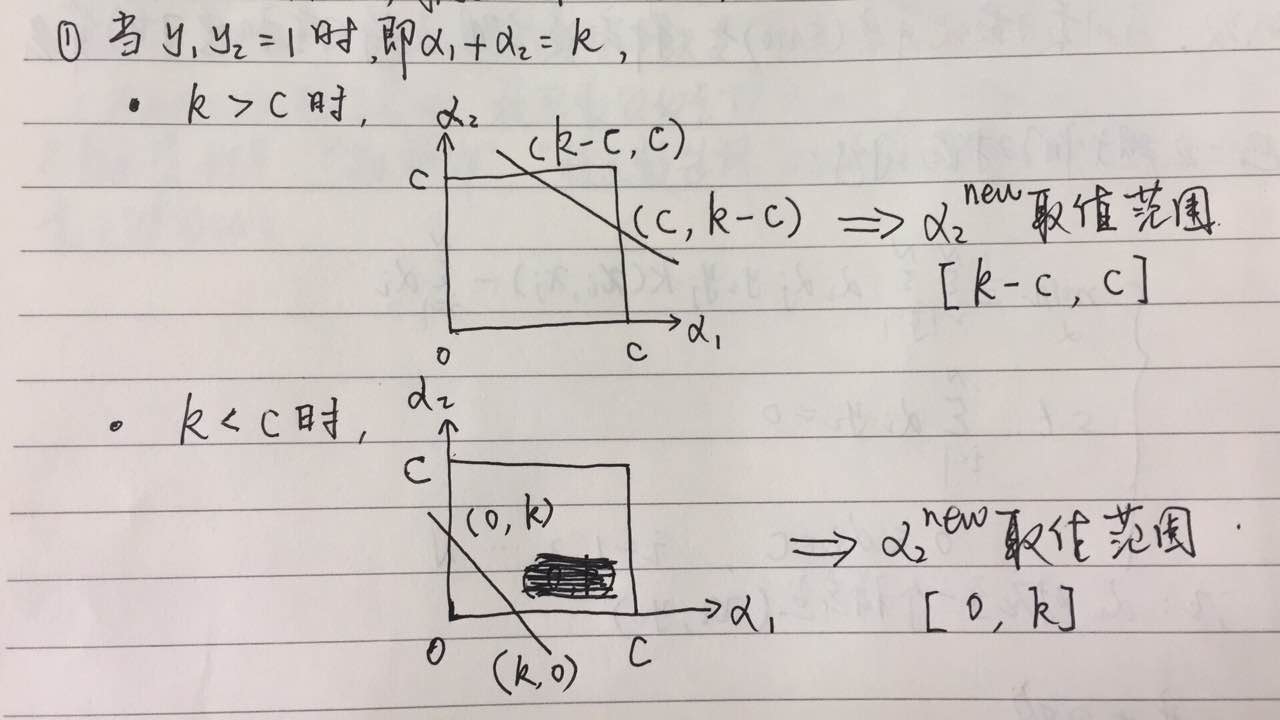
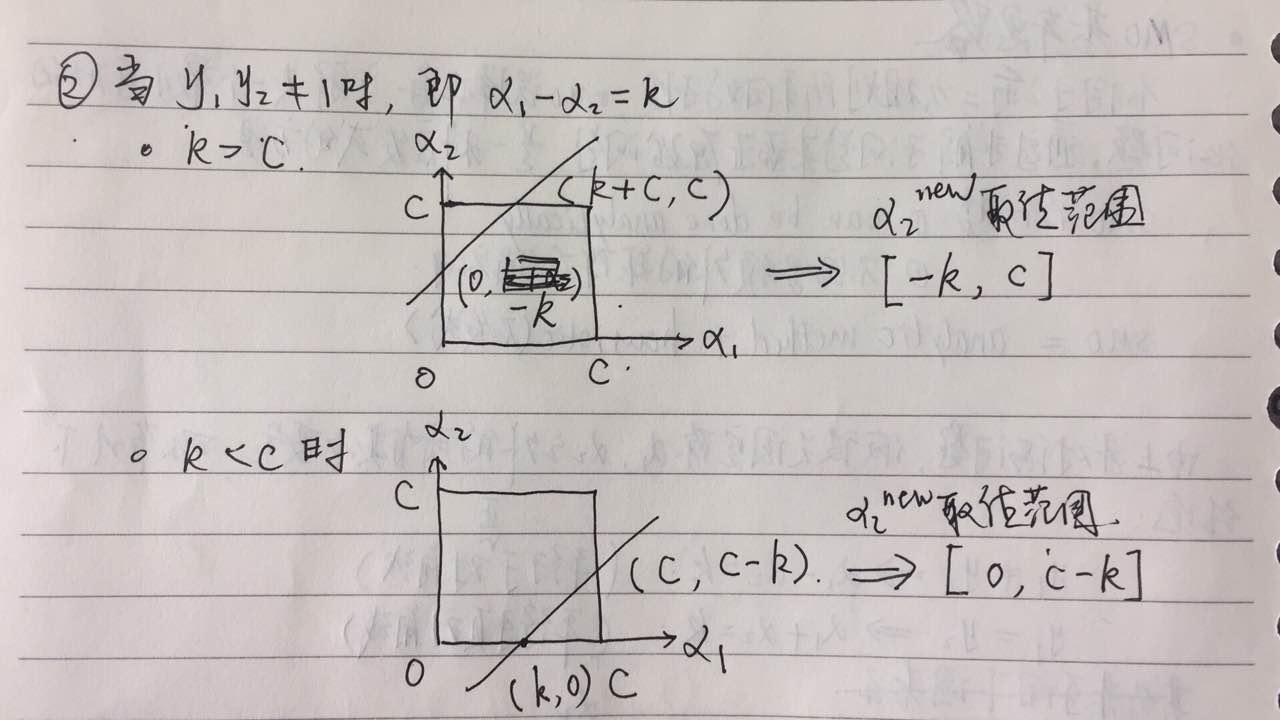
设$L$与$H$是在对角线段端点的上界和下界，由上图所示，要得到$\alpha_2$的准确取值范围，上界我们取两个最大值的最小值，下界取两个最小值的最大值即可。由

由

（2）不考虑约束条件求$\alpha_{2}^{new,unc}$

首先，$\alpha2$的约束条件很多，为了避免求解太繁，我们先不考虑上面两个条件的约束得到$\alpha{2}^{new,unc}$（unc，即uncertain，不确定）的最优解，然后再求约束条件下的最优解$\alpha_{2}^{new}$。

解：

设

令误差

记

故子问题的目标函数可以写为

因为

所以

代入目标函数，得

这样目标函数只有一个未知参数了！针对单变量的凸二次规划问题，这太简单了。

（3）单变量的凸二次规划问题

对$\alpha_2$求导并令其为零

得

将$\alpha_1y_1+\alpha_2y_2=k$代入，得

以下是详细的求解过程：

svm

我们令$\eta=K{11}+K{22}-2K_{12}$，得

再考虑求解约束条件后的$\alpha_{2}^{new}$

（4）考虑求解约束条件$\alpha_{2}^{new}$

因为

所以

于是，我们经过上述的推导，终于就得到了对偶问题子问题的解$(\alpha{1}^{new},\alpha{2}^{new})$。

（5）重新计算$b$和差值$E_i$

在每次完成两个变量的优化后，我们还需要将$\alpha_2^{new}$与$\alpha_2^{old}$比较，如果变化的程度不大，则要重新计算阈值$b$和差值$E_i$

计算阈值b和差值E_i

计算阈值b和差值E_i

3. 基于 Python 实现 SMO 的代码分析

这是基于 Python 实现 SVM 中的 SMO 算法，来自于《机器学习实战》，代码很容易读，基本可以与上文的公式推导完全对应，所以不太理解的地方，还是把 SMO 推导过程的来龙去脉先捋一捋吧！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
from numpy import *
from time import sleep
#==============================================================================
# 打开文件、两个辅助函数
#==============================================================================
# 打开文件逐行读取数据，得到每行的类标签‘labelMat’和数据矩阵‘dataMat’
def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines(): # ‘fr.readlines()’逐行读取数据
        lineArr = line.strip().split('\t') 
        dataMat.append([float(lineArr[0]), float(lineArr[1])]) # 将每行数据的第一个和第二个位置储存到‘dataMat’矩阵
        labelMat.append(float(lineArr[2])) # 每行的第三个是数据标签，存储到‘labelMat’矩阵
    return dataMat,labelMat

# 辅助函数1：取两个不同下标的alpha
def selectJrand(i,m):
    j=i #we want to select any J not equal to i
    while (j==i):
        j = int(random.uniform(0,m))
    return j

# 辅助函数2：用于调整大于H小于L的alpha值，对应alpha2_new的更新法则，alpha2_new只能在[L,H]的区间范围之内	
def clipAlpha(aj,H,L):
    if aj > H: 
        aj = H
    if L > aj:
        aj = L
    return aj

#==============================================================================
# 简化版本SMO算法
#==============================================================================
def smoSimple(dataMatIn, classLabels, C, toler, maxIter): # 5个参数：数据集、类别标签、常数c、容错率、退出前的最大循环次数
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose() # 类别标签‘classLabels’转置为列向量
    b = 0; m,n = shape(dataMatrix) # ‘shape’得到矩阵的行数m和列数n
    alphas = mat(zeros((m,1))) # 初始化alpha为元素全部为零的(m*1)列矩阵
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0 # 用于记录alpha是否已经进行优化
        for i in range(m): # 外层循环
            fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i]) # 计算误差
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)): # 检查变量是否满足KKT条件，如果不满足，那么继续迭代，
                                                                                                                  # 如果满足，那么最优化问题的解就得到了                
                j = selectJrand(i,m) # 内层循环
                fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b # fXj为输入xj的预测值，对应本文公式(7)
                Ej = fXj - float(labelMat[j]) # 预测值与真实值之间的误差
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print "L==H"; continue # 计算eta
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: print "eta>=0"; continue # 求alpha2_new，对应alpha2_new的更新公式，注意eta与文中的符号刚好相反，所以这里是'-='
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                alphas[j] = clipAlpha(alphas[j],H,L)# alpha2_new与alpha2_old比较，如果变化的程度不大，则要更新阈值b和误差值E
                if (abs(alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; continue
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])                                                                       
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) # 打印迭代次数、alpha优化的个数
        if (alphaPairsChanged == 0): iter += 1
        else: iter = 0
        print "iteration number: %d" % iter
    return b,alphas

推荐阅读

  1. 《机器学习》.周志华
  2. 《统计学习方法》.李航
  3. 《机器学习实战》.Peter Harrington
  4. https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-98-14.pdf
------本文结束，欢迎收藏本站、分享、评论或联系作者！------
相关文章
点击查看
赠人玫瑰 手有余香
0%