机器学习算法系列（5）支持向量机（二）

在机器学习算法系列（4）支持向量机（一）我们介绍了线性可分问题的支持向量机方法，不过实际的业务场景中一般不会有那么干净的数据集，有的情况下数据集中的样本是不可分的。但我们要求方法更具有适用性，如果碰到线性不可分问题，我们要适当允许支持向量机容忍一些错误，也就是那条宽宽的“间隔”中允许存在无法归类的数据。

1. 硬还是软？

针对近似线性可分的问题，我们要求所谓的间隔中不能有无法归类的数据，这条间隔比较严格，称之为硬间隔。而对于线性不可分的情形，硬间隔最大化的方法就不适用了，因为一旦间隔区域有异常点，硬间隔的不等式约束不一定都成立。对于不能满足函数硬间隔条件的数据集，需要对硬间隔最大化做一些调整，容许有些许的异常点存在，这样的方法叫做软间隔最大化。

回顾硬间隔最大化的约束最优化问题：

$$\underset{w,b}{max}\ \frac{2}{||w||} \\ s.t.\ y_i(w^Tx_i+b)\ge1,\ i=1,2,...,m.$$

硬间隔最大化的优化问题的约束条件很严格，也就是所有的样本点必须被划分正确。

何谓“软”？也就是将约束条件放松一点点，有些数据破坏了间隔条件是被容许的，但是也不能太多。我们给约束条件加上一个松弛变量$\xi_i$，放宽约束条件，这样硬间隔最大化里面要求的间隔强制为 1 的约束条件就变为：

$$y_i(wx_i+b)\ge1-\xi_i$$

同时，对松弛变量加上惩罚参数 $C\gt0$，惩罚参数的大小控制误分类的容忍程度，目标函数就变为

$$\frac{1}{2}{||w||}^2+C\sum_{i=1}^{N}\xi_i$$

所以线性不可分的支持向量机问题变为凸二次规划问题，我们暂且称为原始问题

$$\underset{w,b,\xi}{min}\quad\frac{1}{2}{||w||}^2+C\sum_{i=1}^{N}\xi_i \\\\ s.t.\quad y_i(wx_i+b)\ge1-\xi_i, \quad\text{$i=1,2,...,N$}\\\\ \xi_i\ge0,\quad\text{$i=1,2,...,N$}\label{origin}$$

2. 转化为对偶问题

同线性可分的问题求解的分析过程一样，对线性不可分的支持向量机凸二次规划问题，依然选择拉格朗日乘子法求解，然后转化为求解对偶问题

（1）首先对原始问题构建拉格朗日函数，$\alpha$ 和 $\mu$ 为拉格朗日乘子

$$L(w,b,\xi,\alpha,\mu)=\frac{1}{2}{||w||}^2+C\sum_{i=1}^{N}\xi_i-\sum_{i=1}^{N}\alpha_i(y_i(wx_i+b)-1+\xi_i)-\sum_{i=1}^{N}\mu_i{\xi}_i \label{lagrangefunction}$$

（2）对偶问题是拉格朗日函数的极大极小问题，先对极小化$L(w,b,\alpha)$，分别对$w,b,\xi$求偏导并令其等于零

$$\frac{\partial L}{\partial w}=w-\sum_{i=1}^{N}\alpha_iy_ix_i=0 \\\\ \frac{\partial L}{\partial b}=\sum_{i=1}^{N}\alpha_iy_i=0 \\\\ \frac{\partial L}{\partial \xi}=C-\alpha_i-\mu_i=0$$

得

$$w=\sum_{i=1}^{N}\alpha_iy_ix_i\\\\ \sum_{i=1}^{N}\alpha_iy_i=0\\\\ C-\alpha_i-\mu_i=0$$

然后将上述三个式子带入拉格朗日函数即可将消去$w$和$b$，即

$$L(w,b,\xi,\alpha,\mu)=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_jx_ix_j+\sum_{i=1}^{N}\alpha_i$$

对偶问题是拉格朗日函数极大极小问题，求上式对$\alpha$的极大化，即得对偶问题

$$max\quad-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_jx_ix_j+\sum_{i=1}^{N}\alpha_i\\ s.t.\quad\sum_{i=1}^{N}\alpha_iy_i=0\\ C-\alpha_i-\mu_i=0\\ \alpha_i\ge0,\mu_i\ge0,i=1,2,...,N$$

当拉格朗日函数转化为其对偶问题的形式之后，需要求解的参数数量下降了，只需要完成对$\alpha$极大化的求解，原始问题$w^{},b^{}$的解可由下式求得，接下来的任务只需要求解$\alpha$了，如下

$$w^{*}=\sum_{i=1}^{N}{\alpha_i}^{*}y_ix_i\\ b^{*}=y_j-\sum_{i=1}^{N}y_i{\alpha_i}^{*}(x_i·x_j)$$

3. 非线性支持向量机与核函数

无论是上一篇讨论线性可分和这篇笔记以上讨论线性不可分问题都属于线性分类问题的范畴，有线性分类势必就有非线性分类，比如如下的动图，在做变化之前的确有一个超平面能把红色和蓝色数据分割开，但是这样的求解往往太麻烦了，如果转换一个角度，对数据做一次转换，原有的非线性问题就变成了线性问题了，求解的难度下降了很多。

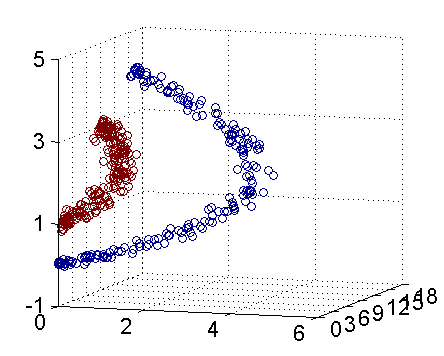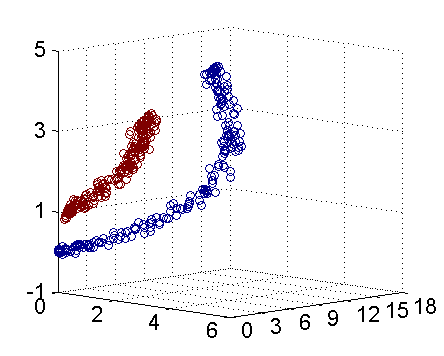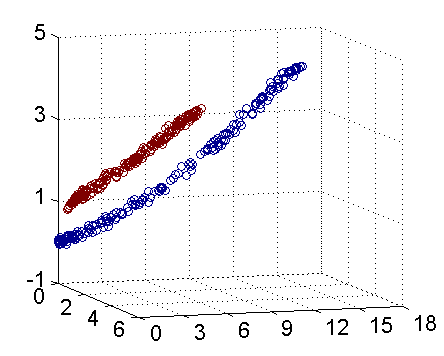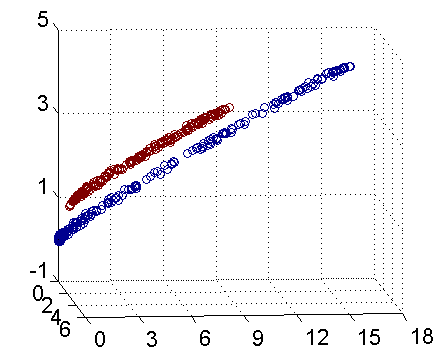
针对非线性分类问题，我们一般使用非线性支持向量机的方法，其主要特点是核技巧（kernel trick）。核技巧的基本想法是通过非线性变换将输入空间（一般是欧式空间或离散集合）映射到另一个特征空间，简单一点理解就是函数变换。

$$\phi(x):x\to\mathcal{H}$$ $$K(x,z)=\phi(x)\cdot\phi(z)$$

其中$K(x,z)$为核函数，$\phi(x)$为映射函数。

因此，当核技巧应用于支持向量机中，对偶问题的目标函数中的内积$(x_i,x_j)$便可以用核函数$K(x,z)=\phi(x)\cdot\phi(z)$来代替，故对偶问题的目标函数变为只有$\alpha$一个参数了：

$$w(\alpha)=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_jK(x_i,x_j)+\sum_{i=1}^{N}\alpha_i$$

对以上问题的求解过程这里就不具体讨论了。

3.1 几种常见的核函数

• 线性核
• 多项式核
• 高斯核（也称RBF核）
• 拉普拉斯核
• sigmoid核

在实际中，我们经常会碰到非线性的分类问题，为了避免复杂的线性变换，这时需要应用核技巧来将数据从低维空间映射到高维空间，然后再采用线性分类器的学习方法训练模型，关于核函数的解释，知乎上的一个回答非常形象机器学习有很多关于核函数的说法，核函数的定义和作用是什么？ - 知乎，这篇文章也值得阅读支持向量机: Kernel « Free Mind。

小结

这篇笔记介绍了软间隔方法和核函数，以及如何将原始问题转化为只有一个参数的对偶问题，这两篇笔记都只提到了如何转换为对偶问题，至于如何求解 ${\alpha_i}$还没有做分析，在接下来的笔记中，我们会学习一种专门对付求解${\alpha_i}$的SMO算法。

推荐阅读

• 《机器学习 Machine Learning》 周志华
• 《统计学习方法》李航 第七章