机器学习算法系列（4）支持向量机（一）

在了解支持向量机（support vector machine，SVM）之前，你可能会对这个算法的名字感到很奇怪，“支持”？“machine”？这到底是啥？没错，你不是一个人，一开始的时候我也是相当纳闷。所以，在正式记录之前我想举一个简单的例子辅助理解。

比如说下图（原谅我自己懒得画图），你就先别管图中的英文注释，如果在一个平面上随机散落了若干方形和圆形的点，现在希望你在方形点和圆形点之间找出一条最宽的间隔，你也可以把这条间隔想象成为一条宽宽的“河流”，然后这条宽宽的间隔又恰好能把河两岸的方形点和圆形点区分开来。

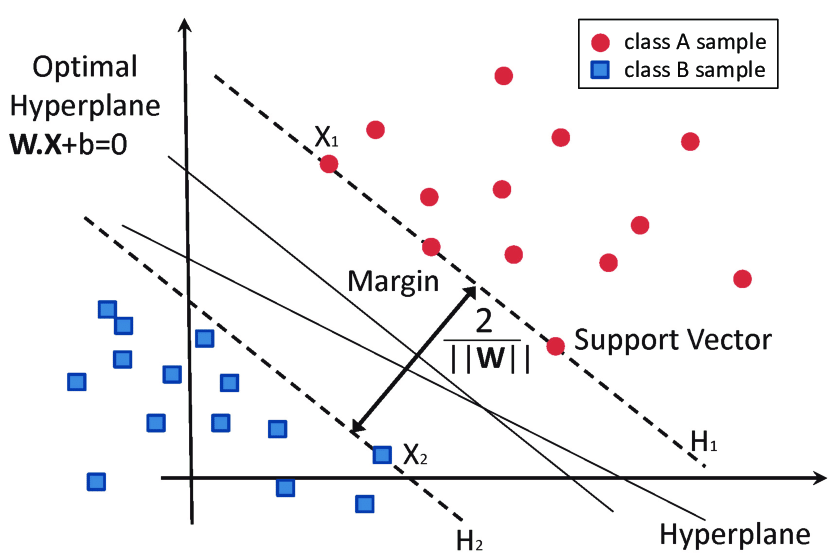
如果把以上的例子看作是分类问题，你会发现跟逻辑回归处理的分类问题思路有区别，逻辑回归会输出一个预测值，然后我们可以通过比较预测值和阈值来确定输出的种类，它属于线性分类器。而刚刚例子中用到的分类方法显然跟逻辑回归是有区别的，它属于非线性的分类器的方法，而这正是支持向量机思想的核心，就是找到一条能把不同点区分开来的宽宽的间隔。

看得出来，上面例子中给的数据是线性可分的，我们可以学习一个线性的分类器，即线性可分支持向量机；当然，现实中的数据不会像例子中的那么完美，当数据是近似线性可分的时候，也可以学习一个线性的分类器，即线性支持向量机；当训练的数据不可分的时候则需要学习非线性支持向量机。伴随着数据越来越复杂，支持向量机的学习方法是从简单到复杂的过程，下面我们来讨论最简单的情形：线性可分支持向量机。

1. 线性可分支持向量机原始问题

支持向量机（Support vector machine， SVM）是一种分类模型，它的任务是在特征空间上找到正确划分数据集的间隔，并且能使几何间隔最大的分离超平面，简而言之，就是要找到一个平面，能够将空间中的点隔开！

首先，回顾中学时代几何中提到的点到直线的距离计算方法：如果我们通过线性方程$w^Tx+b=0$ 来表示空间中的一条直线，将其记为 $(w,b)$。那么空间中任意一点 $(x_i,y_i)$ 到该直线 $(w,b)$ 的几何距离可以表示为

$d=\frac{|w^Tx_i+b|}{||w||}$

前面我们提到过svm的核心思想是在空间中找到正确划分数据的间隔，并且这个间隔当然越宽越好。

那么如何找到使得间隔最大的分离超平面呢？我们先从最简单的情形开始分析，假设超平面$w^Tx+b=0$可以将数据集 100% 正确分类，令

$w^Tx_i+b\ge+1, 为正 \\ w^Tx_i+b\le-1, 为负$

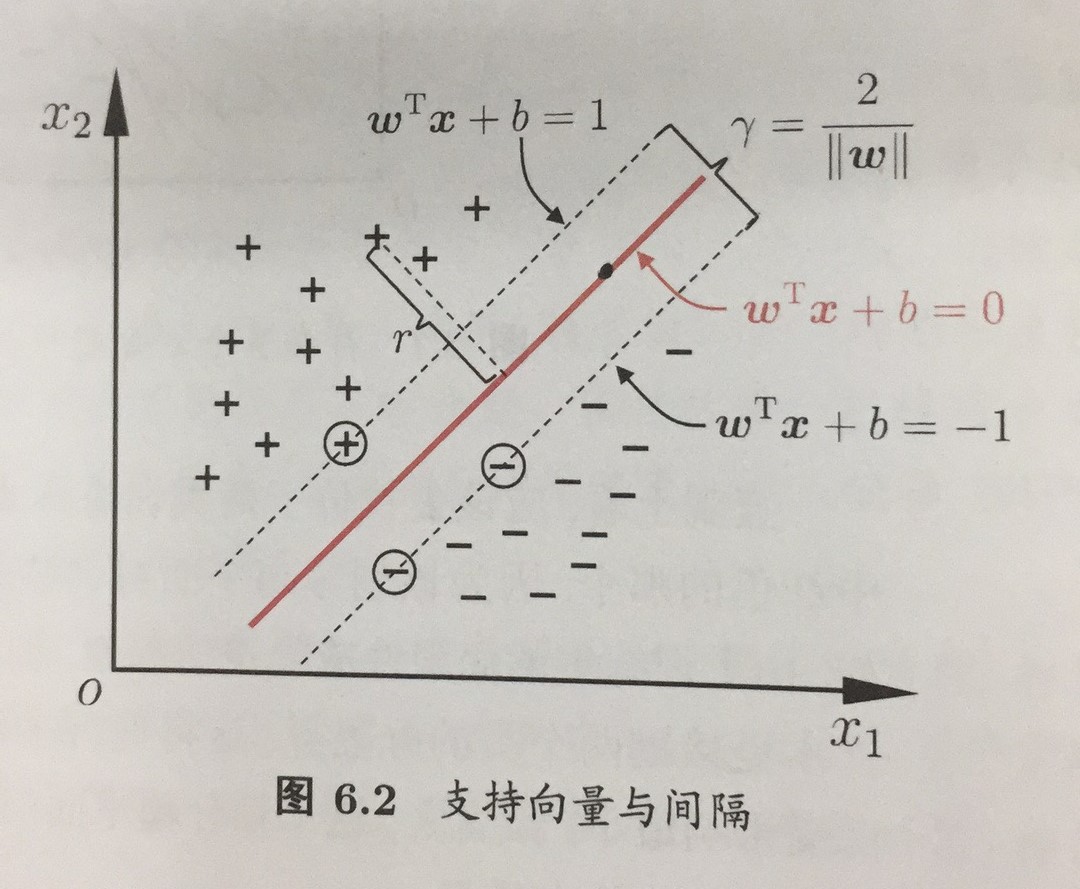
支持向量与间隔

如果我们将可以容忍的间隔设为1，也就是要求距离该平面 $(w,b)$ 几何距离正负为1的空间内没有一个异常点存在，那么寻找最大分离的超平面就意味着上图中两根虚线上的数据点的几何距离$\frac{2}{||w||}$越大越好，转化为数学语言可以表示为如下约束最优化问题：

$\underset{w,b}{max}\ \frac{2}{||w||} \\ s.t.\ y_i(w^Tx_i+b)\ge1,\ i=1,2,...,m.$

在线性可分的情况下，距离分离超平面最近的点称为支持向量，上图中落在虚线上的点就是支持向量，支持向量的决定了分离超平面，一般支持向量的个数不多，往往少数几个训练样本就确定了最终的分离超平面，所以有的时候增加训练样本可能并不会给支持向量机模型的效果带来多少改观。

2. 原始问题转化为对偶问题

我们将线性可分的支持向量机转化为数学语言之后，那么如何求解这个最优化问题呢？

（1）构建拉格朗日函数

该问题的拉格朗日函数可以等价写为（求$\frac{2}{||w||}$的最大值等价于求$\frac{1}{2}{||w||}^2$最小值），$\alpha_i$为拉格朗日乘子

$L(w,b,\alpha)=\frac{1}{2}{||w||}^2-\sum_{i=1}^m{\alpha_i(y_i(w^Tx_i+b)-1)} \label{lagrangefunction}$

这是一个凸二次规划问题，通过拉格朗日乘子法可得到其对偶问题。应用拉格朗日对偶性，原始问题$(w,b)$的对偶问题$(\alpha)$是极大极小问题：

$max\ min\ L(w,b,\alpha)$

分别令拉格朗日函数对$w$和$b$的偏导数为零可得

$w=\sum_{i=1}^m\alpha_iy_ix_i$ $0=\sum_{i=1}^m\alpha_iy_i$

然后将上述两个式子重新代入拉格朗日函数即可将消去$w$和$b$

$L(w,b,\alpha)=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i·x_j)-\sum_{i=1}^{N}\alpha_iy_i((\sum_{j=1}^{N}\alpha_jy_jx_j)x_i+b)+\sum_{i=1}^{N}\alpha_i\\ =\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i·x_j)+\sum_{i=1}^{N}\alpha_i$

然后就得到了原约束问题的对偶问题，即求拉格朗日函数$L(w,b,\alpha)$对$\alpha$的极大

$\underset{\alpha}{max}\ \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i·x_j)\\ s.t.\ \sum_{i=1}^{N}\alpha_iy_i=0\\ \alpha_i\ge0,\ i=1,2,...,N$

故原始问题转化成为了求解对偶问题，为什么要这样做呢？这样做的优点是对偶问题需要求解的参数数量下降，原来需要考虑两个参数 $(w,b)$ ，现在只需要关注 $\alpha$ 便可以了，往往更容易求解。然后可以引入核函数，进而推广到非线性分类问题。设$\alpha^*$是对偶问题的最优化解，那么

$w^*=\sum_{i=1}^m{\alpha_i}^*y_ix_i\\ b^*=y_j-\sum_{i=1}^{N}{\alpha_i}^*y_i(x_i·x_j)$

求得了$w^$，$b^$，也就得到了我们需要的分离超平面。

当然这篇文章主要针对的是线性可分问题，那么线性不可分问题以及对偶问题的求解又怎么解决呢？后面的文章将会继续解释。

我把上述拉格朗日乘子法的求解过程用手写了一遍，辅助理解。

拉格朗日乘子法求解

1. 线性可分支持向量机原始问题

2. 原始问题转化为对偶问题

推荐阅读（建议直接读教材）