1. 基本形式

给定d个属性$x=(x_1;x_2;\cdots;x_d)$，线性模型（linear model）可以表示为一个试图通过属性的线性组合来进行预测的函数：

$f(x)=w^Tx+b$

其中，$x_i$表示属性$x$在第$i$个属性上的取值,$w$直观表达了各个属性在模型预测中的重要性，$w=(w_1;w_2;\cdots;w_d)$。那么，如何求得$w$和$b$便成为了线性回归的主要任务。

Photo by Andre Benz on Unsplash

2. 误差度量（Error Measure）

给定数据集$D={(x1,y_1),(x_2,y_2),\cdots,(x_m,y_m)}$，其中$x_i=(x{i1};x{i2};\cdots;x{id})$，$y_i\in\mathbb{R}$。假设有$d$个属性，线性回归的目标是学得：

$f(x_i)=wx_i+b$

使得$f(x_i)\approx{y_i}$。均方误差是回归任务中最常用的性能度量，因此可以通过让均方误差最小化得到拟合参数

$(w^*,b^*)={argmin}\sum_{i=1}^m(f(x_i)-y_i))^2$

3. 拟合参数

我们可以利用最小二乘法来对$w$和$b$进行估计。为了计算方便，我们将权重和偏置项合并为一个向量$\hat{w}$，维度为（d+1）×1。相应的，将数据集$D$表示为m×（d+1）大小的矩阵$\mathtt{X}$，其中每一行代表一个示例，最后一个元素恒为1，即

$\mathtt{X}= \begin{bmatrix} {x_{11}}&{x_{12}}&{\cdots}&{x_{1d}}&{1}\\ {x_{21}}&{x_{22}}&{\cdots}&{x_{21}}&{1}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\ {x_{m1}}&{x_{m1}}&{\cdots}&{x_{md}}&{1}\\ \end{bmatrix}$

标记值记为$y$，运用最小二乘法(Ordinary Least Square)来估计参数

$E_{\hat{w}^*}=argmin{(y-{\mathtt{X}}{\hat{w}})}^T(y-{\mathtt{X}}{\hat{w}})$

对$\hat{w}$求导得到

$\frac{\partial{E_{\hat{w}}}}{\partial{\hat{w}}}=2\mathtt{X}^T(\mathtt{X}\hat{w}-y)$

令上式为零便可得$\hat{w}$的最优解

${\hat{w}}^*={({\mathtt{X}}^T{\mathtt{X}})}^{-1}{\mathtt{X}}^Ty$

最终，学到的多元线性回归模型为

$f({\hat{x}}_i)={\hat{x}}_{i}^T{({\mathtt{X}}^T{\mathtt{X}})}^{-1}{\mathtt{X}}^Ty$

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression


def plot_linear_regression():
    a = 0.5
    b = 1.0

    # x from 0 to 10
    x = 30 * np.random.random(20)

    # y = a*x + b with noise
    y = a * x + b + np.random.normal(size=x.shape)

    # create a linear regression classifier
    clf = LinearRegression()
    clf.fit(x[:, None], y)

    # predict y from the data
    x_new = np.linspace(0, 30, 100)
    y_new = clf.predict(x_new[:, None])

    # plot the results
    ax = plt.axes()
    ax.scatter(x, y)
    ax.plot(x_new, y_new)

    ax.set_xlabel('x')
    ax.set_ylabel('y')

    ax.axis('tight')


if __name__ == '__main__':
    plot_linear_regression()
    plt.show()

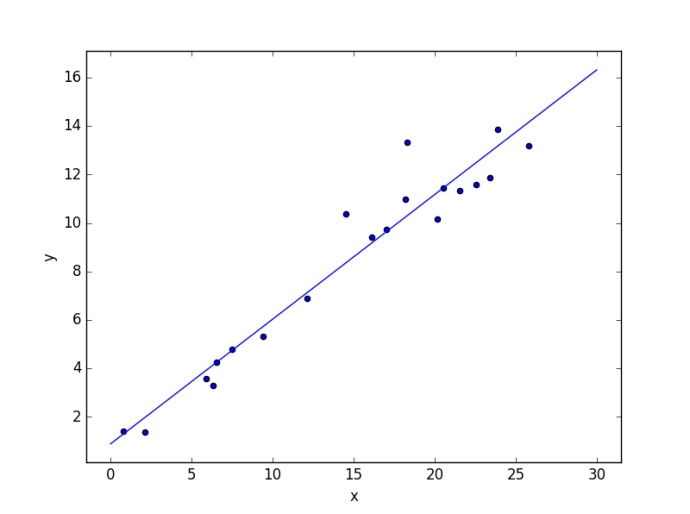
3. 小结

线性回归总的来说比较容易理解，计算上不太复杂。线性回归模型适合于数值型和标称型数据，但是对于非线性的数据拟合效果不佳，比如Andrew Ng的machine learning课程中就提到用线性回归模型做疾病检测的例子，预测的结果很容易受异常值的影响。

机器学习算法系列（2）多元线性回归

1. 基本形式

2. 误差度量（Error Measure）

3. 拟合参数

3. 小结

推荐阅读